Význam a výpočet koeficientu beta
Publikováno: 9.1.2018

Význam koeficientu beta a jeho výpočet, systematické a jedinečné riziko, úprava koeficientu beta pro budoucí prognózy
- riziko
- tržní index
- Blumův model
Koeficient beta patří mezi nejfrekventovanější ukazatele týkající se tržně kotovaných akcií. Investorům poskytuje informaci o riziku akcie vzhledem k trhu. V praxi se používá k oceňování akcií na základě modelu CAPM.
Význam koeficientu beta
Koeficient beta vyjadřuje míru rizika (kolísání výnosu) konkrétní akcie vzhledem k pohybům trhu, který je reprezentován akciovým indexem (např. PX, DAX, S&P 500, NASDAQ, FTSE 100, NIKKEI 225 atd.). Říká, o kolik procent se změní kurz akcie při jednoprocentní změně akciového indexu.
Například beta akcie 1,5 znamená, že při 1% růstu (poklesu) akciového indexu roste (klesá) kurz akcie o 1,5 %.
Finanční teorie člení celkové riziko akcie na jedinečné (nesystematické) a systematické riziko. Celkové riziko akcie měří směrodatná odchylka (rozptyl). Směrodatná odchylka (σ) měří riziko změny (kolísání) výnosnosti akcie, které je způsobeno systematickými a nesystematickými faktory.
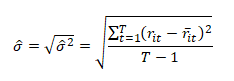
Koeficient beta měří pouze systematické riziko, které nelze v rámci národní ekonomiky diverzifikovat. Zdrojem systematického rizika jsou makroekonomické veličiny (například peněžní zásoba, inflace, úrokové sazby, HDP), politické a sociální události apod. V rámci systematického rizika je nejistota ohledně výnosnosti akcie dána trhem jako celek. Proto je systematické riziko označováno také jako tržní riziko.
Jedinečné riziko akcie souvisí pouze s konkrétní akcií. Nejistota ohledně budoucí výnosnosti je dána činností managementu, používanými technologiemi apod. Jedinečné riziko může být eliminováno diverzifikací, tudíž je zbytečné jej podstupovat. Proto se také označuje jako diverzifikovatelné riziko.
Diverzifikace rizika představuje rozložení investičního rizika mezi více cenných papírů. S rostoucím počtem cenných papírů v investičním portfoliu se snižuje jedinečné riziko a celkové riziko se přibližuje riziku systematickému.
Odhad koeficientu beta
Výpočet koeficientu beta je poměrně jednoduchá záležitost. Výpočet je založen na poměru kovariance výnosnosti i-té akcie a tržního indexu k rozptylu tržního indexu.
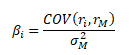
Alternativně lze koeficient beta počítat pomocí korelace, neboť pro její výpočet platí ρ(ri, rM) = COV(ri, rM)/(σi·σM)
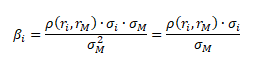
βi ... beta konkrétní akcie, ri ... výnosnost i-té akcie, rM ... výnosnost tržního indexu, COV(ri, rM) ... kovariance výnosnosti i-té akcie a tržního indexu, ρ(ri, rM) ... korelace výnosnosti i-té akcie a tržního indexu, σi ... směrodatná odchylka výnosnosti i-té akcie, σM ... směrodatná odchylka výnosnosti tržního indexu, σM2 ... rozptyl výnosnosti tržního indexu
Zdrojem dat pro výpočet koeficientu jsou skutečné historické výnosnosti i-té akcie a tržního indexu. Proto se takto odhadnutá beta označuje jako tržní historická beta. Odhad historické bety je dán poměrem odhadu kovariance výnosnosti trhu a i-té akcie (σiM) a odhadu rozptylu trhu (σM2) za sledované období T.
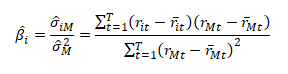
Hodnoty vypočtené bety mají následující význam:
- β = 0 - aktivum je nezávislé na trhu (bezrizikové aktivum)
- 0 < β < 1 - výnosnost i-té akcie roste nebo klesá pomaleji než tržní index (defenzivní akcie)
- β = 1 - výnosnost i-té akcie se chová stejně jako tržní index (neutrální akcie)
- β > 1 - výnosnost i-té akcie roste nebo klesá rychleji než tržní index (agresivní akcie)
Z uvedených hodnot vyplývá, že beta trhu je vždy rovna 1. Hodnoty vyšší než 1 představují vyšší míru systematického rizika než má trh. Naopak hodnoty nižší než 1 představují nižší míru systematického rizika. Prakticky to znamená, že například akcie s β = 1,5 roste na býčím trhu o 50 % rychleji než trh a na medvědím trhu klesá o 50 % rychleji než trh.
Upravený koeficient beta
Odhad historické bety má malou robustnost a tedy i použitelnost pro budoucí období. S úpravou historické bety pro budoucí období přišel americký ekonom Marshall Blume. Ve své úpravě vyšel z předpokladu, že koeficienty beta mají tendenci se přibližovat k betě trhu (β = 1). Budoucí beta vychází ze dvou třetin z historické bety konkrétní akcie a z jedné třetiny z bety trhu.
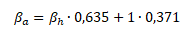
βa ... upravená beta (adjusted), βh ... historická beta (historical)
Uvedená úprava snižuje vysoké hodnoty historické bety agresivních akcií blíže k 1. Zatímco nízké hodnoty historické bety defenzivních akcií zvyšuje blíže k 1.
Výpočet historické a upravené bety
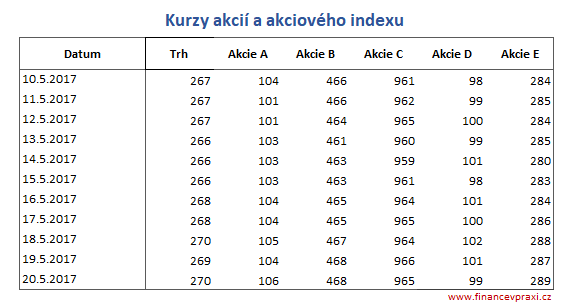
Akciový trh je reprezentován váženým akciovým indexem FvP. Index je vážen tržní kapitalizací 5 kótovaných společností - akcie A (30 %), akcie B (12 %), akcie C (8 %), akcie D (21 %) a akcie E (29 %). Finanční analytik má následující úkoly:
a) vypočítat historické bety akcií
b) vypočítat upravené bety akcií
c) a vypočítat betu trhu
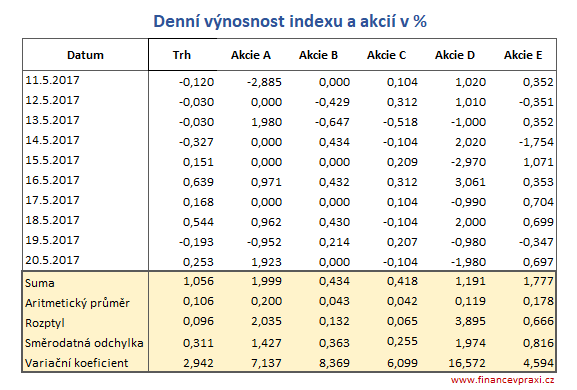
Na základě tržních cen akcií a akciového indexu jsou vypočteny denní změny v %. Z nich jsou pak vypočteny průměrné denní výnosnosti, rozptyly výnosností, směrodatné odchylky a variační koeficienty.
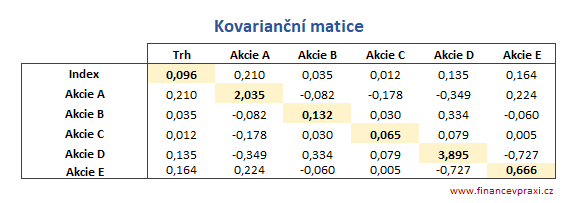
K výpočtu bety je potřeba kovariance akcie a tržního indexu (σiM) a rozptyl výnosnosti tržního indexu (σM2). Kovariance akcií a tržního indexu jsou vypočteny z denních kurzových změn a uspořádány do kovarianční matice. K výpočtu postačí pouze první sloupec nebo první řádek kovarianční matice.
Ad a) historická beta akcie A
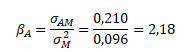
Ad b) upravená beta akcie A
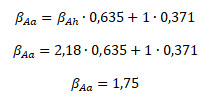
Následující tabulka obsahuje historické bety všech akcií včetně přepočtu na upravené bety.
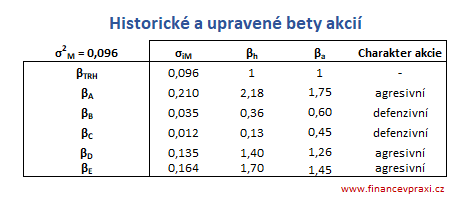
Ad c) beta trhu
Koeficient beta trhu je roven jedné. Tento fakt vyplývá ze samotného výpočtu. Kovariance tržního indexu je rovna jeho rozptylu (σMM = σM2).
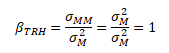
Česko-anglický slovník
- bezrizikové aktivum - risk-free asset
- systematické riziko - systematic risk
- jedinečné (nesystematické) riziko - nonsystematic risk
- diverzifikace rizika - diversification of risk
- nést systematické riziko - bear a systematic risk
- odhad koeficientu beta - estimation of coefficient beta
- historická beta - historical beta
- upravená beta - adjusted beta
- ČÁMSKÝ, F.: Teorie portfolia. Masarykova univerzita 2007, Brno. Druhé přepracované a rozšířené vydání, 123 stran. ISBN 978-80-210-4252-0
- CIPRA, T.: Matematika cenných papírů. Professional Publishing 2013, Praha. První vydání, 288 stran. ISBN 978-80-7431-079-9
- DURČÁKOVÁ, J., MANDEL, M.: Mezinárodní finance. Management Press 2007, Praha. Třetí rozšířené a doplněné vydání, 487 stran. ISBN 978-80-7261-170-6
- KOHOUT, P.: Investiční strategie pro třetí tisíciletí. GRADA Publishing 2010, Praha. Šesté vydání, 296 stran. ISBN 978-80-247-3315-9
- KOHOUT, P., HLUŠEK, M.: Peníze, výnosy a rizika. Příručka investiční strategie. Ekopress 2002, Praha. Druhé rozšířené vydání, 214 stran. ISBN 80-86119-48-3
- MAŘÍK, M. a kol.: Metody oceňování podniku pro pokročilé. Hlubší pohled na vybrané problémy. Ekopress 2011, Praha. První vydání, 548 stran. ISBN 978-80-86929-80-4
- REVENDA, Z., MANDEL, M., KODERA, J., MUSÍLEK, P., DVOŘÁK, P., BRADA, J.: Peněžní ekonomie a bankovnictví. Management Press 2004, Praha. Třetí vydání, 634 stran. ISBN 80-7261-031-7
- SHARPE, W.F., ALEXANDER , G.J.: Investice. VICTORIA PUBLISHING 1994, Praha. Čtvrté vydání, 810 stran. ISBN 80-85605-47-3

