Model CAPM - oceňování kapitálových aktiv

Model CAPM slouží k oceňování kapitálových aktiv na kapitálových trzích. Umožňuje oceňovat jednotlivá aktiva i celá portfolia. Zkratka CAPM vychází z anglického názvu Capital Asset Pricing Model. Zásluhy za model CAPM jsou připisovány W. F. Sharpovi (1964), J. Lintnerovi (1965) a J. Mossinovi (1966).

V rámci modelu CAPM se rozlišují 2 varianty - přímka kapitálového trhu (CML) a přímka cenných papírů (SML). Cílem kapitoly je výklad oceňování jednotlivých akcií (aktiv), proto je pozornost zaměřena pouze přímce SML (Security Market Line).

Model CAPM je založen na následujících předpokladech:

• investoři mají stejný investiční horizont jedno období
• investoři preferují maximální očekávanou výnosnost aktiva (portfolia)
• investoři preferují minimální riziko aktiva (portfolia) počítané směrodatnou odchylkou
• existence bezrizikového aktiva se sazbou r_f, která je pro všechny investory stejná
• aktiva jsou nekonečně dělitelná
• informace jsou volné a snadno dostupné všem investorům
• investoři mají homogenní očekávání - mají stejný postoj k výnosnosti, riziku a kovarianci cenných papírů
• daně a transakční náklady jsou zanedbány

Související kapitoly k modelu CAPM jsou teoretické základy koeficientu beta a praktické výpočty modelu CAPM a koeficientu beta.

Přímka cenných papírů SML

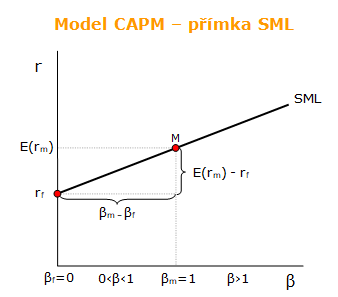
Model CAPM je rovnovážný model, který lze graficky vyjádřit pomocí přímky SML. Přímka SML představuje všechny kombinace výnosových měr akcií a koeficientů beta, při kterých jsou akcie správně oceněny. Model CAPM vyjadřuje střední očekávanou výnosnost i-té akcie pomocí bezrizikové výnosové míry r_f, střední očekávané výnosové míry trhu E(r_M) a koeficientu beta β_i.

Matematický vztah přímky SML pro i-tou akcii lze vyjádřit jako součet bezrizikové výnosové míry a tržní prémie kapitálového trhu násobené koeficientem beta.

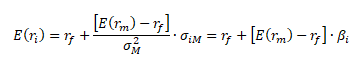
E(r_i) ... střední očekávaná výnosová míra i-té akcie, r_f ... bezriziková výnosová míra, E(r_m) ... střední očekávaná výnosová míra trhu, β_i = σ_iM/σ_M² ... koeficient beta i-té akcie, [E(r_m) - r_f] ... tržní prémie kapitálového trhu

Přímka SML je rostoucí, což odpovídá logice, že rizikovější aktivum by mělo být odměněno nad rámec bezrizikové výnosové míry rizikovou prémií. Majiteli bezrizikového aktiva přísluší bezriziková výnosová míra. Majiteli rizikového aktiva přísluší navíc odměna za podstoupené riziko, které se nazývá riziková prémie

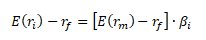
Bezriziková výnosová míra určuje polohu přímky SML. Její výše je nezávislá na pohybech trhu, proto pro ní platí nulová hodnota koeficientu beta (β = 0). Bezrizikovou výnosovou míru lze aproximovat pomocí výnosových měr státních pokladničních poukázek a státních dluhopisů.

Roli střední očekávané výnosové míry kapitálového trhu plní očekávaná výnosnost tržního indexu akciového trhu (např. PX, S&P 500, NIKKEI 225 apod.). Výnosnost tržního indexu vyjadřuje průměrnou míru systematického rizika, proto pro r_M vždy platí β = 1.

Koeficient beta vyjadřuje míru rizika akcie vzhledem k pohybům akciového trhu. Akciový trh je ovlivněn řadou faktorů, jejichž vliv nelze v rámci národní ekonomiky eliminovat. Koeficient beta vyjadřuje míru takového rizika a označuje se jako systematické riziko. Koeficient beta je v rovnici přímky SML jediný faktor, který se váže ke konkrétní akcii.

Nerovnováha v modelu CAPM

Body ležící na přímce SML představují správně oceněné akcie vzhledem k systematickému riziku. Výnosnost správně oceněných akcií vypočítáme pomocí následující rovnice přímky SML

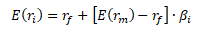
Investor, který aktivně vyhledává nesprávně oceněné akcie, porovnává očekávanou (skutečnou) výnosovou míru i-té akcie (r_i) s její očekávanou rovnovážnou výnosovou mírou [E(r_i)]. Rozdíl se označuje jako koeficient alfa (α_i) a informuje investora o ziskovém potenciálu i-té akcie.

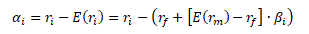
Hodnota koeficientu alfa informuje investora o tom, zda je daná akcie podhodnocená, správně oceněná nebo nadhodnocená. Od hodnoty alfa se odvíjí investiční doporučení.

alfa_i = r_i - E(r_i) > 0 - i-tá akcie je podhodnocená (levná), investiční doporučení je KOUPIT
alfa_i = r_i - E(r_i) = 0 - i-tá akcie je správně oceněná, investiční doporučení je DRŽET
alfa_i = r_i - E(r_i) < 0 - i-tá akcie je nadhodnocená (drahá), investiční doporučení je PRODAT

Body ležící nad přímkou SML představují podhodnocené akcie (aktiva). Zatímco body pod přímkou SML představují nadhodnocené akcie (aktiva).

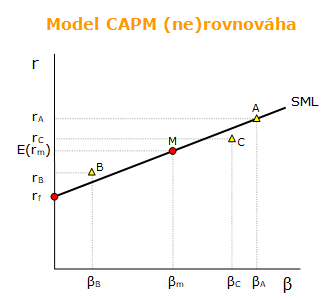
Bod A představuje správně oceněnou akcii, neboť leží na přímce SML. To znamená, že její očekávaná (skutečná) výnosnost se rovná její očekávané rovnovážné úrovni.

Body B a C leží mimo přímku SML a tedy jsou body nerovnováhy. Bod B představuje podhodnocenou akcii, která je trhem přehlížena. Její očekávané (skutečná) výnosnost je vyšší než její očekávaná rovnovážná úroveň. Investoři budou takovou akcii kupovat, čímž dojde k růstu tržní ceny akcie a poklesu její očekávané výnosnosti až na přímku SML. Bod C leží pod přímkou SML a představuje nadhodnocenou akcii, která je trhem překoupena. Racionální investoři budou takovou akcii prodávat, čímž dojde k růst očekávané (skutečné) výnosnosti až na přímku SML, kde bude dosaženo rovnovážné úrovně.

Změna přímky SML

Bezriziková výnosová míra určuje polohu přímky SML. Jestliže se změní její výše, přičemž výnosová míra trhu zůstane stejná, dochází také ke změně sklonu přímky SML. V takové situaci mohou investoři změnit názor na ziskový potenciál jednotlivých akcií a tedy změnit své původní preference.

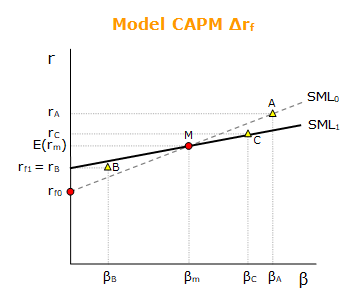
Růst bezrizikové výnosové míry z r_f0 do r_f1 pootočil původní přímku SML₀ do pozice SML₁. Nová rovnováha posunula původně správně oceněnou akcii A mezi podhodnocené akcie vhodné k nákupu. Růst r_f zvýšil ziskový potenciál akcie A. Z původně podhodnocené akcie B je nyní nadhodnocená akcie vhodná k prodeji. A z původně nadhodnocené akcie C je nyní správně oceněná akcie.

Z výše uvedeného vyplývá, že investoři mohou spekulovat na změnu bezrizikové výnosové míry, neboť její změna může vést ke změně investičních příležitostí.