Základní prvky klasických bankovních produktů

Na klientském finančním trhu je nabízeno velké množství finančních produktů stejného charakteru avšak s různými podmínkami. Výběr produktu nemusí být snadný a jednoznačný. Existují však nástroje, které nám rozhodování usnadňují.

Při rozhodování o výběru bankovního produktu hrají klíčovou roli především nominální úrokové sazby a jejich formáty, efektivní úrokové sazby, reálné úrokové sazby, zdanění výnosů a roční procentní sazba nákladů.

Uvedené klíčové parametry se týkají bankovních produktů, kterými jsou spořící účty, termínované účty a spotřebitelské úvěry. V následujícím textu jsou popsány základní prvky těchto produktů, na co si dávat pozor, pomocí čeho se rozhodovat a jak správně vyhodnotit výnosnost výnosového produktu.

Nominální úrokové sazby

Nominální úrokové sazby měří peněžní výnos na korunu uložených nebo investovaných prostředků za určité časové období. Banky u svých produktů deklarují nominální úrokové sazby.

Nominalni úrokové sazby mohou být vyjádřeny v různých formátech dle časového období, na které se vztahují. Například měsíční úrokovou sazbu přepočítáme na roční úrokovou sazbou vynásobením číslem 12.

Úroková sazba dle časového období

Úroková sazba	Symbol	Převod roční úrokové sazby
roční	p. a.	4,000 % p. a.
pololetní	p. s.	2,000 % p. s.
čtvrtletní	p. q.	1,000 % p. q.
měsíční	p. m.	0,333 % p. m.
denní	p. d.	0,011 % p. d.

Pozor je třeba dávat na formáty nominálních úrokových sazeb především u termínovaných vkladů a úvěrů.

V rámci marketingové kampaně je propagován dvouletý termínovaný vklad s úrokovou sazbou 6 %. Úroková sazba se však vztahuje na celé 2 roky. Roční úroková sazba je pak při složeném úročení 2,96 % (= ²√(1 + 0,06) - 1).

Úrokové sazby se mohou ve smlouvě tvářit jako roční, ale v poznámce pod čarou je drobným písmem napsáno, že úroková sazba je například v měsíčním formátu. Tyto praktiky platí zejména pro nebankovní poskytovatele úvěrů.

Efektivní úroková sazba

Efektivní úroková sazba je užitečný nástroj ke srovnávání výnosností spořících a termínových účtů s rozdílnými frekvencemi úročení.

Efektivní úroková sazba vyjadřuje, jaká výše roční úrokové sazby s roční frekvencí připisování úroků odpovídá roční úrokové sazbě s kratší frekvencí připisování úroků než jeden rok (například měsíční).

Platí, že roční úroková sazba s kratší frekvencí připisování úroků je výhodnější než roční úroková sazba s roční frekvencí připisování úroků.

Na základě elementráních úprav jednoduchého a složené úročení lze odvodit vzorec pro efektivní úrokovou sazbu. Principy uročení se zabývá kapitola jednoduché a složené úročení.

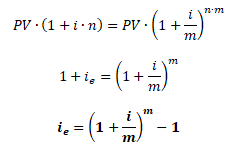
V rámci jednoho úrokového období není důležité, zda je zhodnocení prostředků počítáno pomocí jednoduchého nebo složeného úročení. Oba výsledky jsou v tomto případě stejné. Proto se vzorce pro jednoduché a složené úročení rovnají. Situace se mění v případě roční úrokové sazby s úrokovým obdobím kratším než jeden rok. Efektivní úroková sazba je pak vyšší než deklarovaná nominální úroková sazba.

Praktický výpočet efektivní úrokové sazby

Paní Velká by si ráda otevřela spořící účet, na který by každý měsíc ukládala přebytečné peněžní prostředky. Na trhu jsou tři banky, které nabízí spořící účet s podobnou roční nominální úrokovou sazbou, avšak s rozdílnou frekvencí připisování úroků (= jiné úrokové období). Banky nabízejí spořící účty bez poplatků.

Úkolem je přepočítat roční úrokové sazby na stejnou frekvenci úročení (roční).

Výpočet efektivní úrokové sazby

Zadání/výpočet	Banka A	Banka B	Banka C
Úroková sazba p. a.	4,02 %	4,04 %	3,98 %
Frekvence úročení	pololetní	roční	měsíční
Počet úrokových období	2	1	12
Vzorec	(1 + 0,0402/2)2 - 1	(1 + 0,0404/1)1 - 1	(1 + 0,0398/12)12 - 1
Efektivní úroková sazba p. a.	4,06 %	4,04 %	4,05 %

Nejvýhodnější je nabídka Banky A, která nabízí roční nominální úrokovou sazbu 4,02 % s pololetním připisování úroků. Efektivní úroková sazba říká, že roční úrokové sazbě 4,06 % s ročním připisováním úroků odpovídá roční úroková sazba 4,02 % s pololetním frekvencí připisování úroků. Paní Velká si otevře účet u Banky A.

Vliv zdanění a inflace na úrokové sazby

Banky u svých produktů uvádějí hrubé nominální úrokové sazby. Proto je nutné úrokovou sazbu očistit o zdanění a míru inflace. Teprve pak zjistíme, zda dává smysl uložit peněžní prostředky do daného produktu či nikoliv.

Čistá nominální úroková sazba

Výpočet čisté nominální úrokové sazby spočívá v očištění deklarované úrokové sazby o srážkovou daň z příjmu. V České republice je aktuální sazba daně 15 % (stav roku 2017).

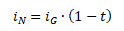
i_N ... čistá úroková sazba, i_G ... hrubá úroková sazba, t ... sazba daně v desetinném čísle

Reálná úroková sazba

Reálná úroková sazba očišťuje nominální úrokovou sazbu o míru inflace. Měří, o kolik více či méně statků a služeb si můžeme reálně koupit.

Kladná reálná úroková sazba představuje reálné zhodnocení uložených prostředků a růst kupní síly. Naopak záporná reálná úroková sazba představuje reálné znehodnocení prostředků a pokles kupní síly.

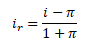
i_r ... reálná úroková sazba, i ... nominální úroková sazba, Π ... míra inflace

Spotřebitelský úvěr

Spotřebitelský úvěr je v České republice upraven zákonem č. 257/2016 Sb., o spotřebitelském úvěru. Spotřebitelským úvěrem se rozumí úvěr poskytnutý spotřebiteli na nákup či rekonstrukci bydlení, na nákup spotřebního zboží a financování služeb.

K výběru spotřebitelských úvěrů se používá ukazatel RPSN (= Roční Procentní Sazba Nákladů). RPSN vyjadřuje procento z dlužné částky za období jednoho roku.

POZOR: Nezaměňujte úrokovou sazbu s RPSN. Úroková sazba vyjadřuje cenu vypůjčených peněz a je součástí ukazatele RPSN. RPSN obsahuje kromě úrokové sazby další výdaje spojené s úvěrem.

Ukazatel shrnuje výdaje spojené s úvěrem do jediného čísla a umožňuje tak porovnávat (ne)výhodnost úvěrů od několika bankovních domů. Výdaje spotřebitele zahrnují splátky úvěrů (jistina a úroky), poplatek za zřízení úvěru, poplatek za vedeni úvěrového účtu atd. Zda však RPSN zahrnuje všechny výdaje spojené s úvěrem doporučuji ověřit u poskytovatele úvěru. Pro kontrolu deklarované výše ukazatele RPSN doporučuji využít RPSN kalkulačku.

Výpočet ukazatele RPSN úvěru na bydlení v MS Excel najdete v článku Jak vypočítat RPSN a vybrat hypotéku.