Model IS-LM: formování rovnováhy - příklady
Publikováno: 23.11.2017

Výpočet rovnic křivek IS a LM a rovnováhy v modelu IS-LM, užití multiplikátorů fiskální a monetární politiky
- model IS-LM
- křivka LM
- křivka IS
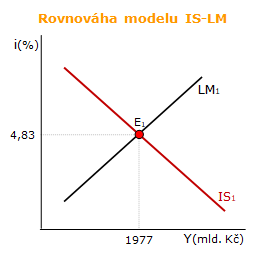
Rovnováha v modelu IS-LM představuje rovnováhu na trhu peněz a na trhu statků a služeb. Rovnováha se nachází v bodě E, který je určen průsečíkem křivek IS a LM. V bodě E se formuje rovnovážný reálný produkt YE a rovnovážná úroková míra iE.
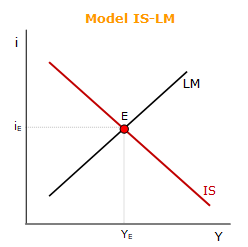
Křivka IS představuje všechny rovnovážné kombinace úrokové míry a reálného produktu, při kterých je trh statků a služeb v rovnováze. Křivka LM představuje všechny kombinace úrokové míry a reálného produktu, při kterých je trh peněz v rovnováze.
Výpočet rovnováhy v modelu IS-LM
Agregátní poptávka je charakterizována následujícími parametry v mld. Kč: C = Ca + 0,8YD, Ca = 300 - 10i, I = 250 - 30i, G = 300, TA = 80, TR = 50, t = 15 %. Poptávka po reálných peněžních zůstatcích je na trhu peněz popsána rovnicí L = 0,3Y - 40i a nabídka peněžních zůstatků (M/P) = 400.
Úkoly:
a) Jaká je rovnice křivky IS?
b) Jaká je rovnice křivky LM?
c) Jaký je rovnovážný reálný produkt (YE) a rovnovážná úroková míra (iE)?
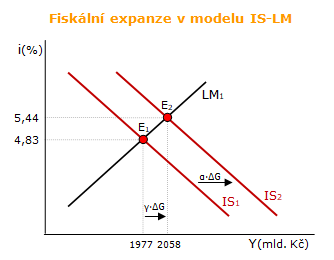
d) Jak fiskální expanze v podobě dodatečných vládních výdajů o 50 mld. Kč změní rovnovážný stav?
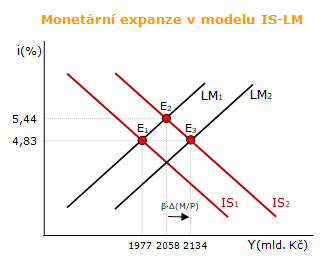
e) Jak monetární expanze v podobě dodatečné nabídky reálných peněžních zůstatků o 47 mld. Kč změní rovnovážný stav?
Body c), d) a e) zobrazit graficky.
Ad a) rovnice křivky IS
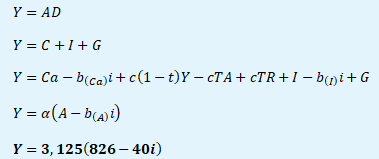
Jednoduchý výdajový multiplikátor třísektorové ekonomiky je 3,125, autonomní výdaje jsou 826 mld. Kč a citlivost autonomních výdajů na úrokovou míru je 40.
Ad b) rovnice křivky LM
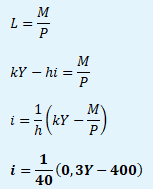
Na základě rovnic křivek IS a LM nyní můžeme přistoupit k výpočtu rovnovážného produktu a rovnovážné úrokové míry.
Ad c) YE, iE = ?
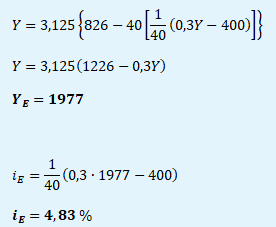
Ad d) fiskální expanze = ΔG = 50 mld. Kč
Multiplikátor fiskální politiky
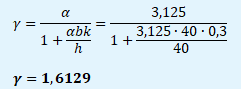
ΔG → ΔYE
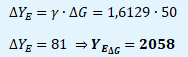
ΔG → ΔiE
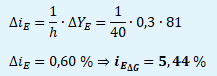
Ad e) monetární expanze = Δ(M/P) = 47 mld. Kč
Multiplikátor monetární politiky
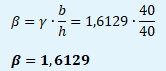
Δ(M/P) → ΔYE
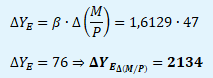
Δ(M/P) → ΔiE
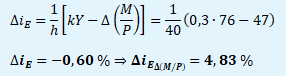
- HOLMAN, R.: Markoekonomie. Středně pokročilý kurz. C. H. Beck 2010, Praha. Druhé vydání, 424 stran. ISBN 978-80-7179-861-3
- MACH, M.: Markoekonomie II pro magisterské (inženýrské) studium. 1. a 2. část. MELANDRIUM 2001, Slaný. Třetí vydání, 367 stran. ISBN 80-86175-18-9
- PROVAZNÍKOVÁ, R., VOLEJNÍKOVÁ, J.: Makroekonomie - cvičebnice. MELANDRIUM 2003, Slaný. Druhé vydání, 379 stran. ISBN 80-86175-23-5
- SAMUELSON, P. A., NORDHAUS, W. D.: Ekonomie. Nakladatelství Svoboda 1995, Praha. Druhé vydání, 1011 stran. ISBN 80-205-0494-X

