Exponenciální funkce a její vlastnosti
Publikováno: 29.5.2017

Vlastnosti exponenciální funkce, graf exponenciální křivky, praktická aplikace modelování exponenciálního trendu
- exponenciální funkce
- exponenciála
- trend
Exponenciální funkce je dána předpisem
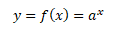
kde y je závisle proměnná, a je základ a x je nezávisle proměnná v exponentu funkce. Pro základ a platí, že je větší než nula a zároveň různý od jedné
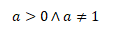
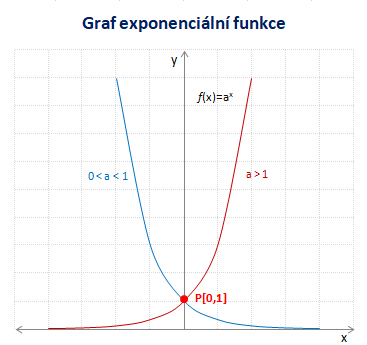
Grafem exponenciální funkce je exponenciála. Exponenciální křivka prochází bodem P[0,1], neboť platí a0 = 1. Pro základ a > 1 je exponcenciální funkce rostoucí, pro 0 < a < 1 je klesající.
Definičním oborem funkce je množina všech reálných čísel, obor funkčních hodnot je omezen nulou a plus nekonečnem
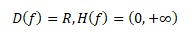
Inverzní funkcí je logaritmická funkce, jejíž definiční obor je omezen nulou a plus nekonečném a oborem funkčních hodnot je množina všech reálných čísel.
Exponenciální funkce je ryze monotónní funkce, neboť je v celém definičním oboru rostoucí nebo klesající. Funkce je prostá a zdola omezená, nemá maximum ani minimum.
Modelování exponenciálního trendu
Exponenciální funkci můžeme využít například ve statistice při modelování exponenciálních trendů. Například prodej nově zavedeného výrobku na trh může v prvních letech růst exponenciálně. K modelování exponenciálního trendu můžeme použít exponenciální funkci ve tvaru
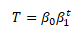
T ... trendová funkce, t ... časová proměnná, β0 a β1 jsou neznámé parametry exponenciální funkce
Exponenciální trendovou funkci je potřeba nejdříve zlinearizovat pomocí logaritmické transformace na tvar
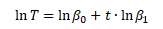
teprve pak je můžeme trendovou funkci odhadnout pomocí metody nejmenších čtverců.
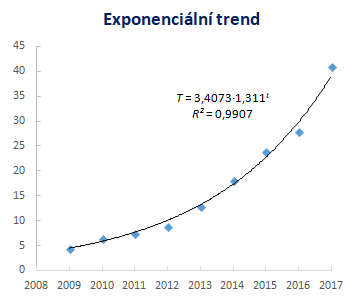
Odhadnutá regresní funkce v logaritmickém tvaru
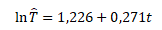
Po zpětné transformaci do původní podoby získáme trendovou exponenciální funkci
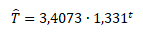
- HINDLS, R., HRONOVÁ, S., SEGER, J., FISCHER, J.: Statistika pro ekonomy. Profesional publishing 2007, Praha. Osmé vydání, 415 stran. ISBN 978-80-86946-43-6
- HUŠEK, R.: Ekonometrická analýza. EKOPRESS 1999, Praha. První vydání, 303 stran. ISBN 80-86119-19-X
- ODVÁRKO. O.: Matematika pro gymnázia. Funkce. Prometheus 1993, Praha. Dotisk čtvrtého vydání, 168 stran. ISBN 978-80-7196-357-8
- POLÁK, J.: Přehled středoškolské matematiky. PROMETHEUS 2015, Praha. Desáté vydání, 659 stran. ISBN 978-80-7196-458-2
- SEIBERT, J., KOLDA, S.: Úvod do studia matematiky na Univerzitě v Pardubicích. Univerzita Pardubice 2004, Pardubice. Deváté vydání, 87 stran. ISBN 80-7194-423-8

