Kvadratická funkce a její aplikace

Kvadratická funkce je polynomická funkce druhého stupně, která je dána funkčním předpisem

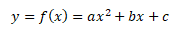
kde y je závisle proměnná, x je nezávisle proměnná a koeficienty a, b, c jsou konstanty.

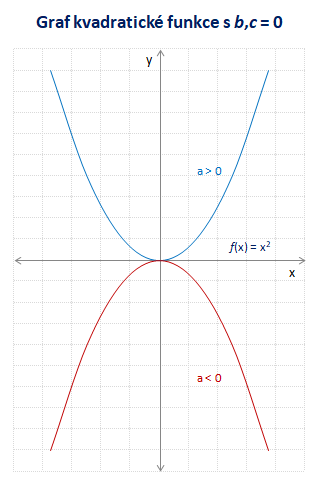
Grafem kvadratické funkce je parabola, která svým tvarem připomíná písmeno U. Pro koeficient a > 0 směřuje vrchol paraboly dolů, pro a < 0 směřuje vrchol paraboly nahoru.

Graf a vlastnosti kvadratické funkce

Nejjednodušší kvadratická funkce bez lineárního a absolutního členu (tj. b, c = 0) má tvar

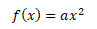
Parabola této funkce je souměrná podél osy y s vrcholem o souřadnicích [0,0]. Taková funkce se označuje jako sudá funkce, tj. funkční hodnoty pro x a -x jsou shodné

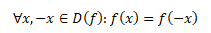
Jestliže k předchozí funkci přidáme nenulovou konstantu c získáme kvadratickou funkci ve tvaru

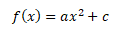
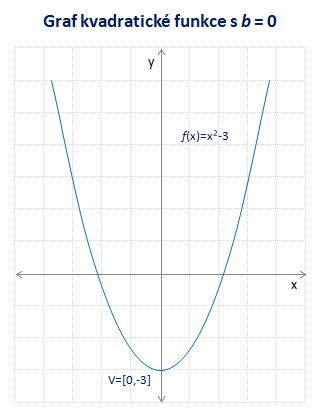
Nenulová konstanta neboli absolutní člen zajistí posun paraboly podél osy y nahoru (kladné c) či dolů (záporné c). Vrchol paraboly se pak nachází v bodě o souřadnicích [0,c]

Konečně se dostáváme ke kvadratické funkci v kompletním tvaru s funkčním předpisem

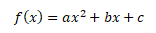
Lineární člen bx zajistí posun paraboly vpravo nebo vlevo. Je-li koeficient b kladný, parabola se posune doleva. Je-li záporný, parabola se posune doprava. Taková funkce již není sudá, protože není souměrná podél osy y.

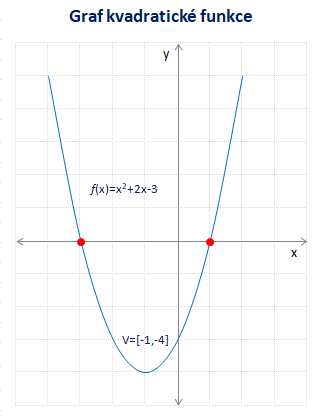
Vrchol paraboly se posunul do bodu [-1,-4]. V tomto a podobných případech můžeme souřadnice vrcholu paraboly vypočítat jako

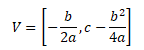
Kořeny kvadratické funkce

Na předcházejícím grafu parabola protíná osu x ve dvou bodech. Tyto dva průsečíky se označují jako kořeny kvadratické funkce. Kořeny kvadratické funkce se počítají dosazením koeficientů kvadratické funkce do následujícího vzorce

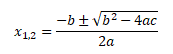
přičemž výraz pod odmocninou se označuje jako diskriminant kvadratické funkce. Hodnota diskriminantu informuje o počtu reálných kořenů kvadratické funkce

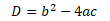
Pro D > 0 existují 2 reálné kořeny, pro D = 0 existuje jeden reálný kořen a pro D < 0 reálný kořen neexistuje.

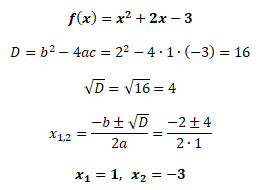
Graf kvadratická funkce protíná osu x v bodech x₁ = 1 a x₂ = -3.

Odhad regresní paraboly

Znalost kvadratické funkce lze v praxi aplikovat na odhad regresní paraboly, který se provádí pomocí metody nejmenších čtverců.

V mikroekonomické teorii má kvadratická funkce uplatnění například v případě celkových tržeb (TR = P·Q) v prostředí nedokonalé konkurence. Cena P je v nedokonalé konkurenci variabilní. Pokud firma snižuje cenu, mohou její tržby růst nebo klesat. Je-li poptávka po produkci firmy elastická, pak při poklesu ceny tržby firmy rostou.

V následujícím grafu jsou na vertikální ose tržby za prodej výrobků a na horizontální ose objem produkce. Se snižováním ceny produkce nejdříve celkové tržby rostou. Od určitého bodu však dochází k poklesu tržeb.

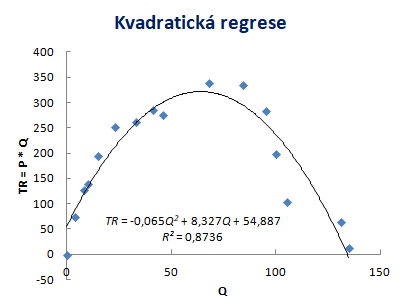
Tržby firmy rostou pouze do určitého bodu. Tento bod se označuje jako lokální maximum tržeb, který lze vypočítat pomocí první derivace odhadnuté funkce

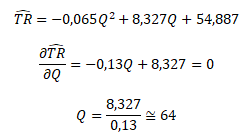
Tržby firmy jsou maximalizovány při výrobě 64 ks výrobků.