Lineární funkce a její aplikace

Lineární funkce je dána předpisem

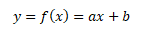
kde y je závisle proměnná, x je nezávisle proměnná, a, b jsou konstanty, přičemž platí a,b ∈ R. Grafem lineární funkce je přímka.

Koeficient a určuje sklon přímky. Je-li a > 0, je přímka rostoucí. V opačném případě je klesající. Koeficient b se označuje jako absolutní člen. Je-li b = 0, pak přímka prochází počátkem. Tento případ se označuje jako přímá úměrnost.

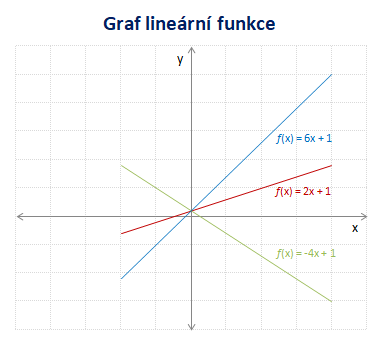
Vlastnosti lineární funkce

Definiční obor lineární funkce i obor funkčních hodnot jsou množiny reálných čísel

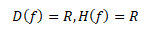
Lineární funkce není omezená zdola ani shora, nemá maximum ani minimum. Funkce je rostoucí nebo klesající a tedy prostá. Není sudá ani lichá.

Prostá a inverzní funkce

Funkce f je prostá, jestliže každé dvojici různých hodnot z definičního oboru odpovídají různé funkční hodnoty

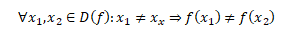
Ke každé prosté funkci f existuje funkce inverzní f^-1. Pro inverzní funkci platí

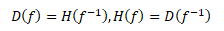
Inverzní funkce vznikne vyjádřením x jako závisle proměnné a y jako nezávisle proměnné

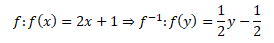
Poloha a sklon přímky

Koeficient b určuje polohu přímky v bodě x = 0, tj. udává průsečík přímky s osou y

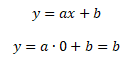
Sklon přímky je určen koeficientem a. K výpočtu sklonu přímky je potřeba znát 2 body funkce [x₁, f(x₁)] a [x₂, f(x₂)], tj. libovolné x₁ a x₂ z definičního oboru, kterým jsou přiřazeny funkční hodnoty f(x₁) a f(x₂)

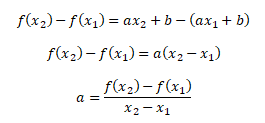
Odhad regresní přímky

Znalost lineární funkce lze v praxi aplikovat na odhad regresní přímky, který se provádí pomocí metody nejmenších čtverců.

Typickým příkladem regresní přímky je jednoduchá keynesiánská spotřební funkce, která sleduje závislost spotřebních výdajů C na běžném příjmu domácnosti Y. Body v grafu (modré značky) vyjadřují vztah mezi spotřebou a příjmy, který je proložen regresní přímkou (černá přímka).

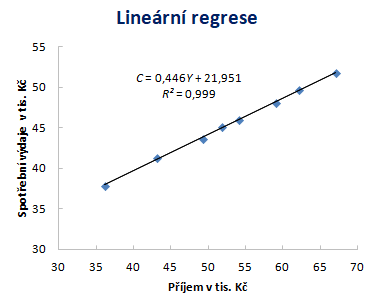
Odhadnutá regresní přímka spotřebních výdajů pak má podobu

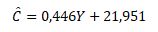
kde koeficient a je roven 0,446 a koeficient b je roven 21,951.