Nepřímá úměrnost a rovnoosá hyperbola

Nepřímou úměrnost představuje každá funkce, která je dána předpisem

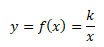
kde y je závisle proměnná, k je konstanta různá od nuly a x je nezávisle proměnná. S rostoucím x funkční hodnoty stále klesající a limitně se přiblížují k nule. Grafem nepřímé úměrnosti je rovnoosá hyperbola.

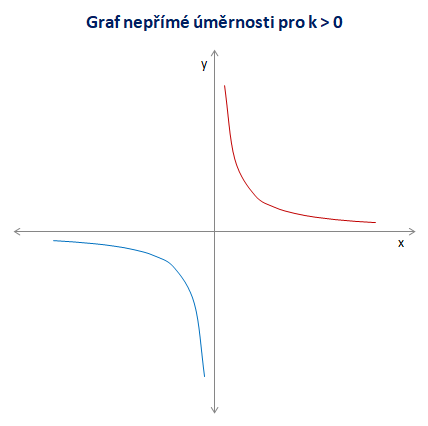
Vlastnosti funkce pro k > 0

Pro k > 0 je definiční obor funkce i obor funkčních hodnot dán množinou reálných čísel různých od nuly

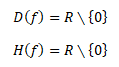
Funkce je klesající v intervalu (-∞,0) a (0,+∞). Funkce není omezená zdola ani shora. Je lichá, neboť je symetrická vzhledem k počátku.

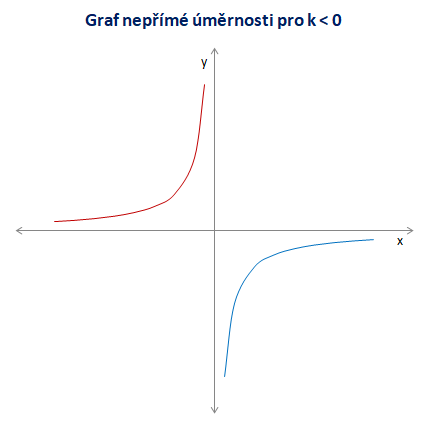
Vlastnosti funkce pro k < 0

Pro k < 0 je definiční obor a obor funkčních hodnot identický jako v předchozím případě. Funkce je rostoucí v intervalu (-∞,0) a (0,+∞). Funkce není omezená zdola ani shora. Je lichá, neboť je symetrická vzhledem k počátku.

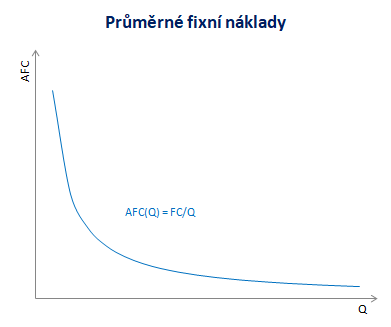
Průměrné fixní náklady

Tvar rovnoosé hyperboly má v mikroekonomii například křivka fixních nákladů v krátkém období.

Fixní náklady firmy jsou náklady, které musí být hrazeny nezávisle na objemu produkce. Musí být hrazeny i při nulovém produktu. Jedná se o náklady na fixní výrobní faktory (např. nájem výrobní budovy, pronájem stroje apod.).

Jsou-li fixní náklady FC rozpočítány na různé objemy vyrobené produkce Q jsou průměrné fixní náklady klesající

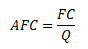
Uvedený vztah platí pouze pro k > 0 a kladné hodnoty x resp. Q. Jinak by to nedávalo smysl.