Úvod do regresní analýzy

Regresní analýza je statistický nástroj, který slouží k modelování vztahů mezi proměnnými a tvorbě predikcí. Regresní modely nabývají různých tvarů matematických funkcí, které se označují jako regresní funkce. Regresní funkce obsahuje 2 skupiny proměnných - závisle proměnnou y a množinu nezávisle proměnných x₁, x₂, ...., x_k, které vysvětlují variabilitu y.

Lineární regresní model

Lineární regresní model vyjádřuje stochastickou závislost závisle proměnné y na regresní funkci základního souboru η a náhodné složce ε

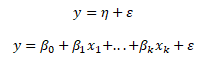
y ... závisle proměnná, η ... regresní funkce základního souboru, ε ... náhodná složka, β_k ... neznámé regresní parametry, x_k ... nezávisle proměnné

Regresní funkce základního souboru (populace) je teoretický koncept, který obsahuje neznámé parametry β₀, β₁, ..., β_k. Parametry β_k jsou výsledkem vztahů v celé populaci, kterou v naprosté většině případů nemáme k dispozici.

V praxi pracujeme s výběrem dat z určitého základního souboru, proto se musíme spokojit s výběrovými odhady b₀, b₁, ..., b_k neznámých parametrů

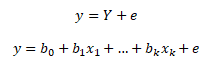
y ... závisle proměnná, Y ... výběrová regresní funkce, e ... odhad náhodné složky, b_k ... odhad parametrů modelu, x_k ... nezávisle proměnné

Výběrové odhady parametrů se statisticky verifikují. Potvrdí-lí se u nich optimální vlastnosti, pak je můžeme vztáhnout na celou populaci.

Stejně tak se musíme v praxi spokojit s odhadem náhodné složky ε. Odhad náhodné složky se označuje jako reziduum e, které je rozdílem mezi skutečnou hodnotou závisle proměnné y a její vyrovnanou hodnotou Y.

Tvary regresních funkcí

Regresní modely nabývají různého stupně složitosti. Obecně se rozlišují jednofaktorové regresní modely a vícefaktorové regresní modely.

Modely s jednou nezávisle proměnnou se označují jako jednofaktorové regresní modely - lineární, kvadratický, hyperbolický, odmocniný, mocninný, exponenciální a logaritmický

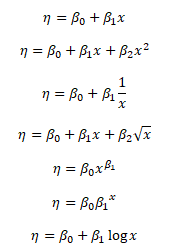
Naopak modely s více nezávisle proměnnými se označují jako vícefaktorové regresní modely - mnohonásobný lineární model, mocniný a exponenciální

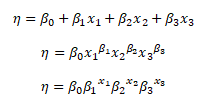
Průběh závislosti mezi 2 proměnnými lze identifikovat pomocí grafického diagramu (bodový graf). V případě vícenásobné regrese je identifikace složitější. Průběh závislosti mezi více proměnnými již nelze zobrazit graficky. Ideální specifikace modelu se volí na základě statistických testů průkaznosti modelu.

Metoda nejmenších čtverců

Pro odhad parametrů klasického lineárního regresního modelu (KLRM) se používá metoda nejmenších čtverců (MNČ). MNČ je použitelná pouze pro modely s lineárními regresními parametry. Lze jí však použít i pro modely s nelineárními parametry, které je možné vhodnou transformací linearizovat (například logaritmická transformace).

Cílem MNČ je nalézt vhodnou aproximační funkci, která nejlépe vystihuje empirické hodnoty závisle proměnné. Nejlepší aproximační funkce je taková funkce, která nejlépe minimalizuje reziduální součet čtverců odchylek skutečných hodnot závisle proměnné y od teoretických η. V praxi je teoretická hodnota nahrazena vyrovnanou hodnotou Y odhadnutou pomocí výběrové regresní funkce.

Složkové vyjádření KLRM

Metoda nejmenších čtverců je založena na minimalizaci součtu čtverců odchylek. Minimalizační kritérium MNČ má podobu

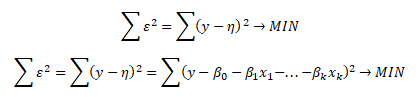
Parciálními derivacemi minimalizačního kritéria podle jednotlivých parametrů modelu β₀, β₁, ..., β_k a položením rovnic rovných nule vytvoříme soustavu normálních rovnic. Soustava obsahuje tolik rovnic, kolik je parametrů v modelu. V následujícím příkladě je odvození soustavy normálních rovnic pro výběrovou kvadratickou regresní funkci

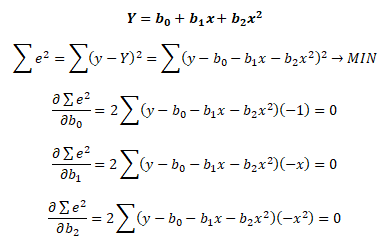
Úpravami získáme následující finální podobu soustavy normálních rovnic.

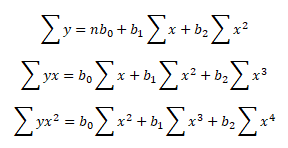
Bodové odhady b_j parametrů β_j lze získat řešením soustavy normálních rovnic pomocí Cramerova pravidla.

Maticové vyjádření KLRM

Pro složitější modely jsou Cramerovy vzorce nepřehledné. Proto doporučuji řešit soustavu normálních rovnic v maticové podobě. Maticové vyjádření klasického lineárního regresního modelu je přehlednější a prostorově úspornější.

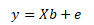
y ... sloupcový vektor n pozorování hodnot závisle proměnné, X ... matice n x (k + 1) pozorování hodnot vysvětlujících proměnných, β ... sloupcový vektor k + 1 neznámých parametrů, e ... sloupcový vektor n náhodných složek → e = y - Xβ

Derivací minimalizačního kritéria podle transponovaného vektoru b^T získáme soustavu normálních rovnic, ze které nakonec vyjádříme bodovou odhadovou funkci MNČ

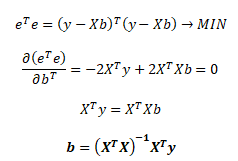
b ... sloupcový vektor bodových odhadů parametrů β, X^T ... transponovaná matice (k + 1) x n nezávisle proměnných, (X^TX)^-1 ... inverzní čtvercová matice (k + 1) x (k + 1), y ... sloupcový vektor závisle proměnné

Bodové odhady vektoru b parametrů β doporučuji ideálně provádět pomocí ekonometrického softwaru například Gretl nebo v MS Excelu.