Rozptyl a směrodatná odchylka
Publikováno: 21.4.2017

Vzorce pro výpočet rozptylu a směrodatné odchylky, výpočet variability výnosností akcií a akciového indexu
- rozptyl
- směrodatná odchylka
- akcie
Rozptyl a směrodatná odchylka jsou v teorii i praxi nejčastěji používané míry variability analyzovaných veličin. Měří proměnlivost (variabilitu) empirických hodnot okolo jejich střední hodnoty (aritmetického průměru).
Rozptyl
Rozptyl je definován jako průměrná čtvercová odchylka veličiny od střední hodnoty. Pro výpočet rozptylu základního souboru (populace) σ2 se používá vzorec
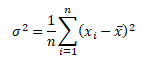
n ... počet pozorování, xi ... konkrétní realizace veličiny X, x ... prostý aritmetický průměr veličiny X
Většinou se však setkáme s výběrovým rozptylem s2. V praxi máme k dispozici pouze výběrový vzorek dat ze základního souboru dané veličiny. Proto se používá modifikovaný vzorec rozptylu pro počet pozorování n < 30
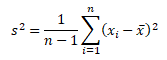
Při větším počtu pozorování je rozdíl mezi σ2 a s2 zanedbatelný.
Směrodatná odchylka
Směrodatná odchylka se počítá jako druhá odmocnina z rozptylu. Stejně jako u rozptylu se rozlišují populační směrodatná odchylka σ
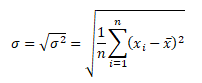
a výběrová směrodatná odchylka s
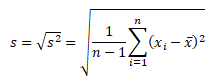
Hodnota směrodatné odchylky je lépe interpretovatelná než hodnota rozptylu. Ve finanční teorii je směrodatná odchylka považována za riziko změny výnosnosti aktiva. Vyjadřuje průměrnou lineární vzdálenost skutečných výnosností od jejich střední hodnoty.
Výpočet rozptylu a směrodatné odchylky
Akciový trh je reprezentován akciovým indexem, který je vážen tržní kapitalizací 5 kótovaných společností - akcie A (30 %), akcie B (12 %), akcie C (8 %), akcie D (21 %) a akcie E (29 %).
Úkolem je:
a) vypočítat rozptyly z denních výnosností akcií a indexu
b) vypočítat směrodatné odchylky
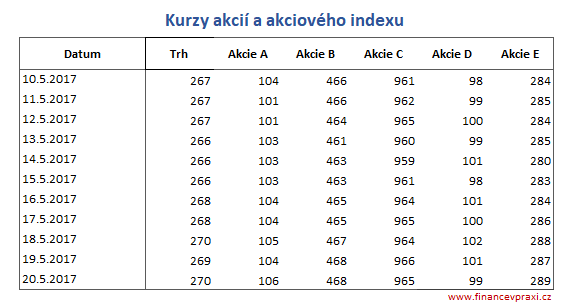
Z tržních cen akcií a akciového indexu jsou vypočteny denní změny v %. Z nich pak jsou vypočteny průměrné výnosnosti, rozptyly, směrodatné odchylky a variační koeficienty.
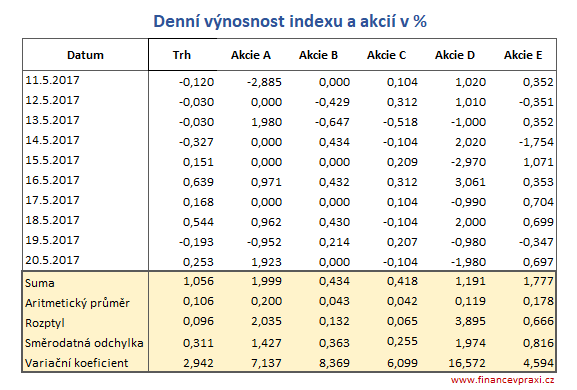
Rozptyl denních výnosností akciového indexu (sloupec Trh) vypočítáte z denních výnosností a průměrné denní výnosnosti
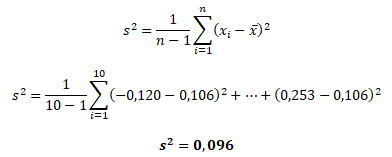
a směrodatnou odchylku indexu jako druhou odmocninu z rozptylu indexu
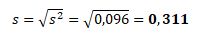
Stejným způsobem vypočítate rozptyl například akcie A
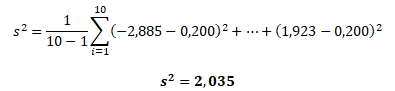
a směrodatnou odchylku akcie A
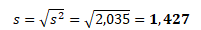
Funkce v MS Excel
- PRŮMER() - vrátí aritmetický průměr vybraných hodnot
- VAR() - vrátí rozptyl základního souboru
- VAR.VÝBĚR() - vrátí výběrový rozptyl vybraných hodnot
- SMODCH() - vrátí směrodatnou odchylku základního souboru
- SMODCH.VÝBĚR() - vrátí výběrovou směrodatnou odchylku vybraných hodnot
- CYHELSKÝ, L., KAHOUNOVÁ, J., HINDLS, R.: Elementární statistická analýza. Management Press 2001, Praha. Druhé doplněné vydání, 319 stran. ISBN 80-7261-003-1
- HINDLS, R., HRONOVÁ, S., SEGER, J., FISCHER, J.: Statistika pro ekonomy. Profesional publishing 2007, Praha. Osmé vydání, 415 stran. ISBN 978-80-86946-43-6

