Testování koeficientu korelace
Publikováno: 28.5.2017

Výpočet korelace a její testování pomocí kritéria Studentova rozdělení, testování korelace v příkladech
- koeficient korelace
- Studentovo rozdělení
- korelační matice
Vysoká hodnota koeficientu korelace nemusí znamenat statisticky průkaznou závislost veličin. Aby bylo možné vztáhnout výběrovou korelaci na celou populaci, tj. mezi náhodnými veličinami X a Y existuje statisticky významná závislost, je nutné vypočtené koeficienty korelace otestovat na základě testových kritérií.
Koeficient korelace
Korelace ρ(X,Y) měří lineární závislost mezi veličinami X a Y a standardizuje hodnoty kovariance. Počítá se jako poměr kovariance C(X,Y) veličin X a Y k součinu směrodatných odchylek D(X)·D(Y) veličin X a Y.
Při výpočtu koeficientu korelace se rozlišuje populační koeficient korelace ρxy
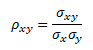
ρx,y ... populační koeficient korelace, σxy ... kovariance veličin x a y, σx, σy ... směrodatné odchylky veličin x a y
a výběrový koeficient korelace rxy
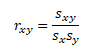
rx,y ... výběrový koeficient korelace (n < 30), sxy ... kovariance veličin x a y, sx, sy ... výběrové směrodatné odchylky veličin x a y (n < 30)
Výběrový koeficient korelace se používá k odhadu populačního protějšku pro malé rozsahy dat (n < 30). Abychom mohli řící, že je odhad rxy věrohodný, je nutné koeficient otestovat na zvolené hladině statistické významnosti.
Koeficient korelace může nabývat hodnot na intervalu ⟨-1;+1⟩. Hodnoty blízké +1 představují silnou pozitivní závislost veličin. Naopak hodnoty blízké nule poukazují na nezávislost (nekorelovanost) veličin. A nakonec hodnoty blízké -1 představují silnou negativní závislost.
Hodnoty |rxy| > 0,8 představují silnou korelaci veličin. Zatímco hodnoty |rxy| < 0,3 představují slabou korelaci veličin. Slabá korelace veličin nemusí znamenat nezávislost veličin. Může mezi nimi však existovat jiná než lineární závislost.
Testové kritérium
K testování statistické významnosti korelačních koeficientů se používají testová kritéria s různým pravděpodobnostním rozdělením. Nejpoužívanější je však Studentovo rozdělení t s n - 2 stupni volnosti, které je předmětem této kapitoly.
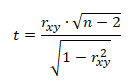
Test o nezávislosti
Při testování statistické významnosti korelačního koeficientu je testována nulová hypotéza H0: ρ = 0 o nezávislosti veličin X a Y proti alternativní hypotéze H1: ρ ≠ 0 o závislosti veličin X a Y. Testovací kritérium je vyhodnocováno porovnáním absolutní hodnoty testovacího kritéria |t| s tabelovanou hodnotou t1-α/2(n - 2).
Jestliže |t| > t1-α/2(n - 2) je koeficient rxy statisticky významný.
Jestliže |t| < t1-α/2(n - 2) je koeficient rxy statisticky nevýznamný.
Testování korelace v praxi
Následující korelační matice je sestavena z párových koeficientů korelace denní výnosnosti akciového trhu. Zeleně obarvené koeficienty korelace jsou větší než 0,4 (|rxy| > 0,4) a představují středně silnou korelaci výnosnosti indexu a akcií.
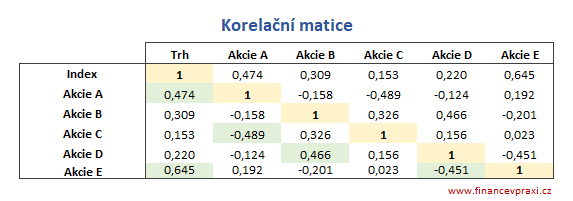
Úkolem je otestovat koeficienty korelace r21 = 0,474 a r61 = 0,645 na 5% hladině statistické významnosti. Tabelovanou hodnotu t statistiky Studentova rozdělení lze vypočítat v MS Excel pomocí statistické funkce TINV(0,05;8). Vstupní data pro výpočet t statistiky jsou
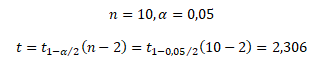
První testovaný koeficient korelace r21 = 0,474 reprezentuje vztah lineární závislosti mezi akcií A a trhem
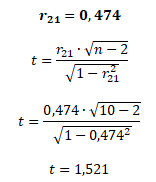
Absolutní hodnota t-statistiky je nižší než tabelovaná hodnota: |t| < t → 1,521 < 2,306. Koeficient korelace je statisticky nevýznamný, tj. mezi akcií A a trhem neexistuje lineární závislost.
Další testovaný koeficient korelace r61 = 0,645 reprezentuje vztah lineární závislosti mezi akcií E a trhem
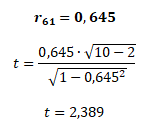
Absolutní hodnota t-statistiky je vyšší než tabelovaná hodnota: |t| > t → 2,389 > 2,306. Mezi akcií E a trhem existuje statisticky průkazná pozitivní lineární závislost.
- CYHELSKÝ, L., KAHOUNOVÁ, J., HINDLS, R.: Elementární statistická analýza. Management Press 2001, Praha. Druhé doplněné vydání, 319 stran. ISBN 80-7261-003-1
- ČÁMSKÝ, F.: Teorie portfolia. Masarykova univerzita 2007, Brno. Druhé přepracované a rozšířené vydání, 123 stran. ISBN 978-80-210-4252-0
- JAROŠOVÁ, E., PECÁKOVÁ, I.: Příklady k předmětu statistika B. Vysoká škola ekonomická 2003, Praha. První vydání, 222 stran. ISBN 80-245-0015-9
- MINAŘÍK, B.: Statistika II. Mendelova zemědělská a lesnická univerzita v Brně 2007, Brno. První vydání, 136 stran. ISBN 978-80-7375-033-6

