Mocninná funkce s přirozeným exponentem
Publikováno: 27.5.2017

Vlastnosti mocninné funkce se suchým a lichým exponentem, grafy sudé a liché funkce, inverzní funkce
- mocninná funkce
- kubická parabola
- odmocniná funkce
Mocninná funkce je polynomická funkce n-stupně, která je dána funkčním předpisem
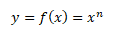
kde y je závisle proměnná, x je nezávisle proměnná a n je exponent. Přičemž platí, že x může být libovolné reálné číslo (x ∈ R) a exponent n patří do oboru přirozených čísel N. Taková funkce se označuje jako mocninná funkce s přirozeným exponentem.
Grafem mocninné funkce pro n = 1 je přímka, pro n = 2 kvadratická parabola, pro n = 3 kubická parabola a pro n > 3 parabola n-tého stupně
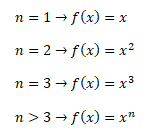
U mocninných funkcí se rozlišuje sudá a lichá hodnota přirozeného exponentu, s čímž souvisí odlišný graf dané funkce a vlastnosti.
Funkce s lichým exponentem
Pro n-liché platí, že definičním oborem funkce i oborem funkčních hodnot je množina reálných čísel
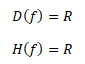
Funkce není omezená shora ani zdola, je rostoucí pro všechny přirozená lichá n a tedy prostá. Grafem této funkce je kubická parabola n-tého stupně.
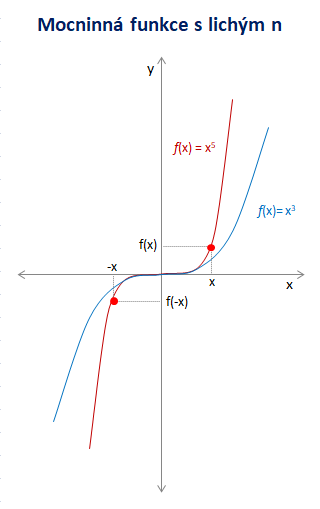
Typickou vlastností mocninné funkce s lichým exponentem je, že její graf je symetrický vzhledem k počátku. Taková funkce se označuje jako lichá funkce. Pro funkční hodnoty f(x) liché funkce platí
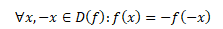
Funkce se sudým exponentem
Pro n-sudé je definičním oborem množina reálných čísel a obor funkčních hodnot je zdola omezen nulou
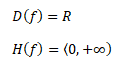
Funkce je klesající na intervalu (-∞; 0⟩ a rostoucí na intervalu ⟨0, +∞). Na těchto intervalech je funkce prostá. Tyto funkce jsou sudé a mají tvar písmene U, který je typický pro kvadratickou funkci.
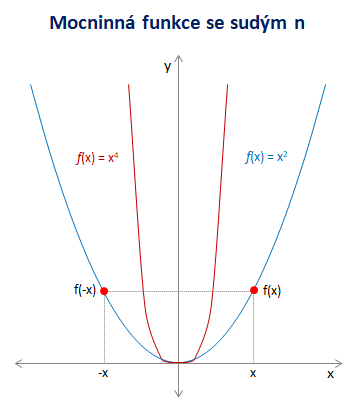
Typickou vlastností funkce se sudým exponentem je, že její graf je symetrický podle osy y. Taková funkce se označuje jako sudá funkce. Pro funkční hodnoty f(x) sudé funkce platí
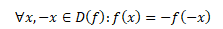
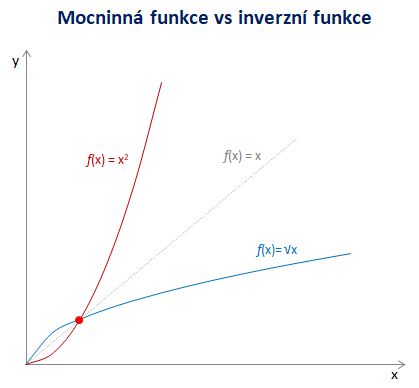
Odmocninná funkce
Ke každé prosté funkci f existuje funkce inverzní f-1. Prostá funkce je každá funkce, která je rostoucí nebo klesající.
Mocninná funkce pro n-liché je rostoucí v celém svém definičním oboru. Naopak funkce pro n-sudé je klesající na intervalu mínus nekonečná do nuly a rostoucí od nuly do plus nekonečna.
Odmocninná funkce je inverzní funkce k mocninné funkci s přirozeným exponentem
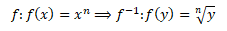
Pro n = 2 a s prohozenými x a y získáme inverzní funkci
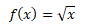
přičemž funkce dává smysl pouze pro první kvadrant, tj. x větší nebo rovno nule
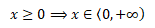
Funkce v MS Excel
- POWER(číslo; exponent) ... vrací umocněné číslo na zadaný exponent
- ODVÁRKO. O.: Matematika pro gymnázia. Funkce. Prometheus 1993, Praha. Dotisk čtvrtého vydání, 168 stran. ISBN 978-80-7196-357-8
- POLÁK, J.: Přehled středoškolské matematiky. PROMETHEUS 2015, Praha. Desáté vydání, 659 stran. ISBN 978-80-7196-458-2
- SEIBERT, J., KOLDA, S.: Úvod do studia matematiky na Univerzitě v Pardubicích. Univerzita Pardubice 2004, Pardubice. Deváté vydání, 87 stran. ISBN 80-7194-423-8
- VOSMANSKÁ, G.: Matematika. Mendelova zemědělská a lesnická univerzita v Brně 2007, Brno. Páté nezměněné vydání, 120 stran. ISBN 978-80-7375-079-4

