Předpověď budoucí hodnoty FORECAST.LINEAR()

V praxi může nastat situace, kdy je potřeba odhadnout budoucí hodnotu sledované veličiny. Aby měl odhad nějakou vypovídací hodnotu, musí být založen na statisticky průkazném modelu. Jinak nelze považovat předpovědi za věrohodné. Analytik by si tedy měl být vědom rizik, které může prosté dosazení dat do excelovské funkce přinést.

Pro rychlou a orientační krátkodobou předpověď budoucí hodnoty můžete v excelu použít funkci FORECAST.LINEAR(), která je založena na lineárním vztahu mezi veličinami.

Funkce FORECAST.LINEAR()

Funkce patří do kategorie statistických funkcí, která v roce 2016 nahradila funkci FORECAST(). Kvůli kompatibilitě se staršími verzemi můžete používat obě funkce.

Funkce vrácí budoucí hodnoty závisle proměnné y na základě lineárního vztahu s nezávisle proměnnou x

=FORECAST.LINEAR(x; pole_y; pole_x)

Do parametru X se zadává očekávaná hodnota nezávisle proměnné, parametr Pole_y slouží k zadání oblasti dat s empirickými hodnotami závisle proměnné a parametr Pole_x slouží k zadání empirických hodnot nezávisle proměnné.

Odhad budoucích hodnot je založen na lineární regresní funkci odhadnuté pomocí metody nejmenších čtverců.

Lineární trend

Úkolem je prodloužit lineární trend čistého zisku o jedno období dopředu. Nezávisle proměnnou x je v tomto případě čas t, který je reprezentován narůstajícím počtem období stejně jako sloupec Rok.

=FORECAST.LINEAR(t₂₀₁₈;hodnoty X;hodnoty Y)

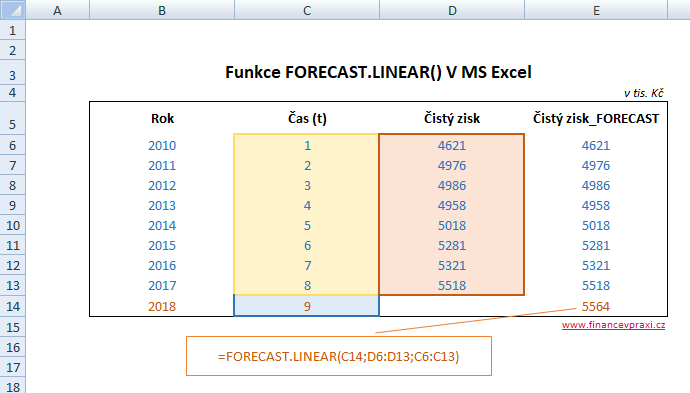
Na následujícím spojnicovém grafu je oranžovou barvou zvýrazněna bodová předpověď čistého zisku pro rok 2018 ve výši 5.564 tis. Kč.

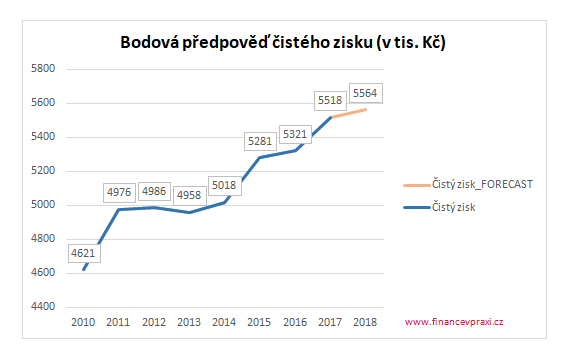
Bodová předpověď je však příliš striktní. Z toho důvodu doporučuji bodovou předpověď doplnit o interval spolehlivosti například s 95% pravděpodobností. Horní mez intervalu pak může představovat optimistický scénář vývoje a dolní mez intervalu pesimistický scénář.

Předpověď lineární regrese

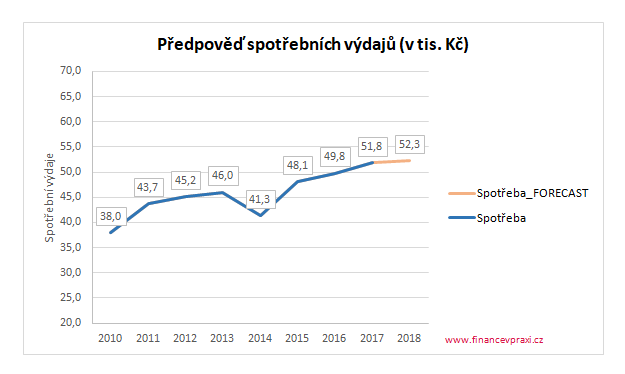
Ve druhém případě je zkoumán vztah mezi průměrným měsíčním příjmem a spotřebními výdaji jednotlivce v jednotlivých letech. Výše čistého příjmu ovlivňuje výši spotřebních výdajů. Vztah mezi 2 proměnnými lze obecně identifikovat na základě bodového diagramu.

Bodový diagram najdete na kartě Vložení → v sekci Grafy → graf Bodový.

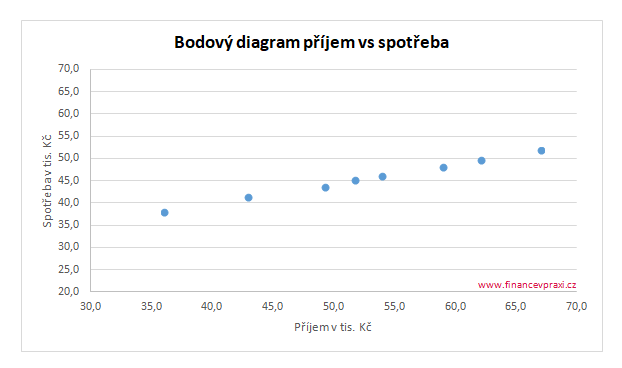
Body v grafu ukazují na lineární závislost mezi proměnnými, kterou můžeme vyjádřit přímkou. Funkce FORECAST.LINEAR() je tedy vhodná pro odhad budoucí hodnoty.

Nyní můžeme odhadnout spotřební výdaje na jedno období dopředu na základě očekávaného průměrného příjmu ve výši 68 tisíc Kč.

=FORECAST.LINEAR(68;hodnoty X;hodnoty Y)

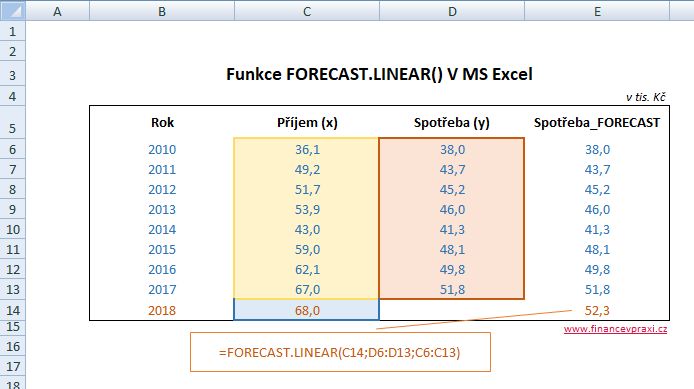
Bodová předpověď měsíčních spotřebních výdajů spotřebitele je pro rok 2018 opět zvýrazněna oranžovou barvou.