Detekce autokorelace náhodné složky

Kapitola navazuje na Regresní přímku a Cramerovo pravidlo, kde byl odhadnut model lineární závislosti průměrné měsíční spotřeby na průměrném měsíčním příjmu spotřebitele v jednotlivých letech.

Úkolem je nyní analyzovat reziduální složku výběrové regresní přímky z hlediska sériové nezávislosti pomocí grafického vývoje v čase, autoregresního modelu procesu AR(1) a Durbin-Watsonova testu.

Testování autokorelace v praxi

V modelu regresní přímky vystupují spotřební výdaje spotřebitele jako závisle proměnná y a příjem spotřebitele jako nezávisle proměnná x. Model regresní přímky reprezentuje jednoduchý model spotřební funkce spotřebitele. Následující tabulka obsahuje realizace proměnných y a x, vyrovnané hodnoty Y a vypočtené hodnoty reziduální složky e.

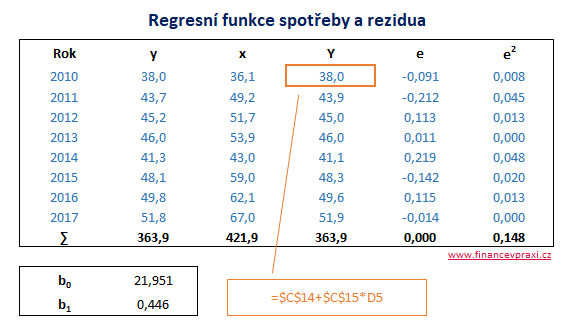
Výběrová regresní přímka s odhady parametrů b₀ a b₁ má podobu

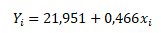
Víme, že skutečná hodnota závisle proměnné y je dána stochastickou závislostí na vyrovnané hodnotě Y a reziduální složce e

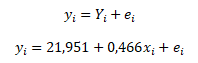
Z uvedeného vztahu dopočítáme hodnoty reziduální složky pro jednotlivé roky podle

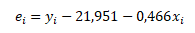
například hodnota rezidua pro rok 2017 je

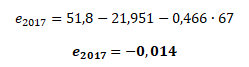
Získaná rezidua dále použijeme pro zobrazení grafického vývoje v čase, výpočet autokorelačního koeficientu procesu AR(1) a Durbin-Watsonova testu.

Grafická analýza reziduí

Z následujícího grafu vývoje reziduí v čase je patrné časté překřížení časové osy. Rezidua, která často střídají znaménka, jsou podezřelá z negativní autokorelace.

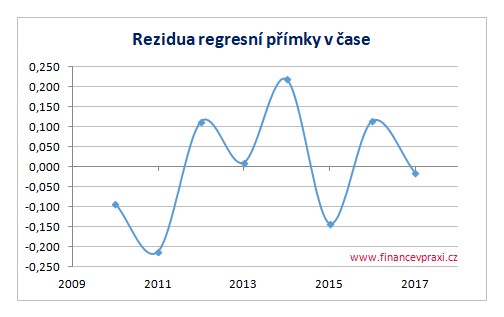
Potvrdit či vyvrátit podezření reziduální složky z negativní autokorelace nám pomůžou následující testy.

Autokorelační koeficient ρ

Nejčastější formou autokorelační struktury náhodné složky je autokorelace prvního řádu, kterou lze popsat pomocí autoregresního procesu AR(1)

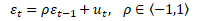
ρ ... autokorelační koeficient prvního řádu, u_t ... normálně rozdělená náhodná složka

Je-li koeficient ρ na zvolené hladině statisticky významný, pak je náhodná složka sériově závislé. V praxi pracujeme s výběrovým odhadem r parametru ρ

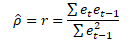
Následující tabulka obsahuje hodnoty reziduí a upravené hodnoty reziduí pro odhad výběrového autokorelačního koeficientu prvního řádu.

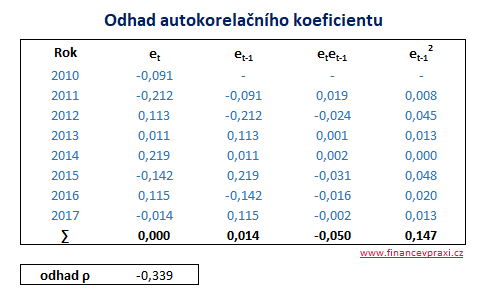
Záporná hodnota odhadu r indikuje možnost negativní autokorelace

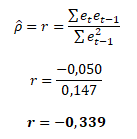
Abychom mohli vyhodnotit statistickou významnost parametru r a tedy významnost autokorelace, musíme nejdříve odhadnout rozptyl reziduální složky s²

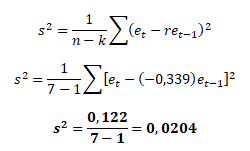
a inverzní matici (X^TX)^-1, kterou vytvoříme ze zpožděných hodnot reziduální složky o jedno období (X^TX)^-1

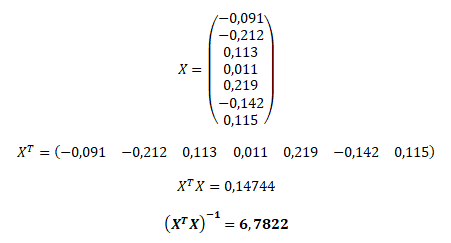
Standardní chybu odhadu r získáme jako odmocninu součinu s² a (X^TX)^-1, kterou použijeme pro testování statistické významnosti autokorelace

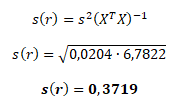
Na základě t-testu nyní můžeme rozhodnout o statistické (ne)významnosti odhadu autokorelačního koeficientu

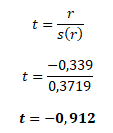
Absolutní hodnotu vypočteného testu porovnáme s kvantilem Studentova rozdělení t_1-α/2(n - k) na 5% hladině významnosti. Hodnotu kvantilu zjistíme ve statistických tabulkách nebo v excelu pomocí funkce TINV()

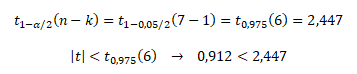
Na 5% hladině významnosti zamítáme hypotézu o statistické významnosti neboli s 97,5% pravděpodobností považujeme odhad autokorelačního koeficientu za statisticky nevýznamný. Jinými slovy, hodnoty reziduální složky nejsou sériové závislé.

Výpočet Durbin-Watsonova testu

Následující tabulka obsahuje rezidua a upravená rezidua v čase t-1. Z nich pak jsou propočítány výrazy v čitateli a jmenovateli Durbin-Watsonova testu.

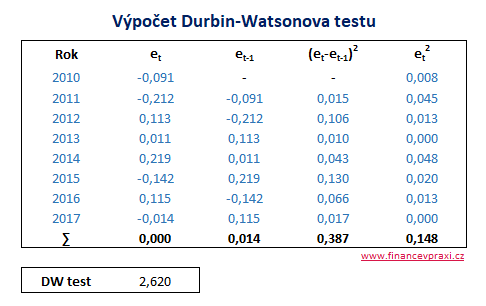
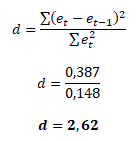
Výsledek Durbin-Watsonova testu je vyšší než 2. Z toho můžeme předběžně usuzovat na negativní autokorelaci reziduální složky. K přesnému posouzení výsledku použijeme tabulkové hodnoty pro dolní d_L a horní d_U meze, které vymezují intervaly autokorelace, nulové autokorelace a šedé zóny pro daný počet pozorování n a počet nezávisle proměnných k.

Odhad výběrové regresní přímky spotřební funkce je založen na n = 8 a k = 1. Ve statistických tabulkách jsou pro uvedené hodnoty d_L = 0,76 a d_U = 1,33.

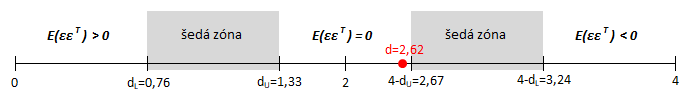
Durbin-Watsonův test potvrdil nulovou autokorelaci reziduální složky. Reziduální složka modelu tedy není sériové závislá.

Shrnutí testů reziduální složky

Z provedených testů sériové nezávislosti reziduální složky máme jednoznačný výsledek. Grafický vývoj hodnot reziduální složky v čase sice poukazoval na negativní autokorelaci, ale odhad autokorelačního koeficientu procesu AR(1) a Durbin-Watsonův test negativní autokorelaci vyvrátily.

Odhad náhodné složky regresního modelu můžeme prohlásit za sériově nezávislý. To znamená, že odhady regresních parametrů jsou nestranné a jejich rozptyly zůstávají také vydatné.