Autokorelace náhodné složky

V předchozích kapitolách byly vysvětleny postupy pro testování jednotlivých regresních parametrů a základní metody pro testování modelu jako celku. Dalším krokem statistické verifikace regresního modelu je testování odhadů náhodné složky z hlediska sériové nezávislosti, která je jedním z požadavků metody nejmenších čtverců (MNČ).

Cílem kapitoly je popis nejčastěji používaných diagnostických nástrojů pro detekci sériové závislosti, kterými jsou autoregresní model AR(1), Durbin-Watsonův test a Durbinovo h.

Náhodná vs reziduální složka

V regresní analýze základní souboru jsou hodnoty závisle proměnné y_i dány stochastickou závislostí teoretické regresní funkce η_i a náhodné složky ε_i. Hodnoty náhodné složky jsou pak rozdíly mezi skutečnými a teoretickými hodnotami

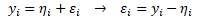
Hodnoty náhodné složky však v praxi neznáme, a proto si pomáháme aproximací pomocí reziduální složky e_i. Reziduální složka je produktem výběrové regresní analýzy. Je dána rozdílem mezi skutečnými hodnotami závisle proměnné y_i a vyrovnanými hodnotami Y_i

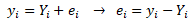
Reziduální složka je pak ovlivněna zvoleným regresním modelem odhadnutým metodou nejmenších čtverců.

Význam autokorelace náhodné složky

Autokorelace znamená závislost hodnot jedné veličiny na sobě samé. V našem případě se jedná o závislost hodnot náhodné složky ε_t v čase t na předchozích hodnotách ε_t-s v čase t-s, přičemž platí t ≠ s. Autokorelace se projevuje zejména v čase. Existenci autokorelace náhodné složky lze řešit pomocí metody zobecněných nejmenších čtverců.

Nejčastější forma autokorelační struktury je autokorelace prvního řádu. To znamená, že hodnoty náhodné složky ε_t jsou závislé na bezprostředně předcházejících hodnotách ε_t-1. Existují i autokorelace vyššího řádu, ale ty nejsou předmětem kapitoly.

Požadavky MNČ na náhodnou složku

Klasickými požadavky metody nejmešních čtverců jsou sériová nezávilost náhodné složky a konstatní a konečný rozptyl náhodné složky. Oba požadavky můžeme shrnout do jednoho z předpokladů MNČ ve vektorovém tvaru

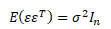
σ² ... rozptyl náhodné složky, I ... jednotková matice

Pro jednoduchost si uvedený předpoklad MNČ rozepíšeme na tříprvkovém vektoru ε. Střední hodnota součinu vektoru ε a transponovaného vektoru ε^T představuje kovarianční matici, kterou můžeme dále upravit jako jako součin konstatního rozptylu a jednotkové matice

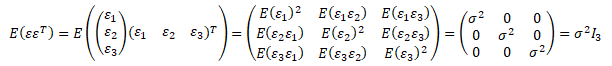
Kovarianční matice je symetrická a obsahuje párové koeficienty kovariance, které vyjadřují míru lineární závislosti mezi dvěmi veličinami. Požadavkem je, aby kovariance mimo diagonálu matice byly nulové. Nulové kovariance představují nezávislost veličin.

Na hlavní diagonále kovarianční matice leží konstantní rozptyl náhodné složky. Platí totiž, že kovariance stejné veličiny je rovna jejímu rozptylu E(ε_tε_t) = σ². Vytknutím konstantního rozptylu σ² z kovarianční matice získáme matici jednotkovou.

Příčiny a důsledky autokorelace

Nejčastějšími příčinami autokorelace náhodné složky bývají setrvačnost ve vývoji ekonomických časových řadách, chybná specifikace modelu a zahrnutí zpožděné endogenní a exogenní proměnné mezi vysvětlující proměnné modelu.

Je-li porušen požadavek sériové nezávislosti náhodné složky, nemají odhady MNČ parametrů β optimální vlastnosti. Odhady MNČ sice zůstávají nestranné, ale jejich rozptyl již není minimální a tedy nejsou vydatné, ani asymptoticky vydatné (n → ∞). V takovém případě se nemůžeme na odhadnutý model spolehnout a použít pro předpovědi modelu.

Identifikace autokorelace

Autokorelaci prvního řádu lze identifikovat pomocí grafického vývoje reziduální složky v čase. Potvrdit či vyvrátit existenci autokorelace však můžeme až na základě testovacích statistik, kterými jsou například autokorelační koeficient procesu AR(1), Durbin-Watsonův test a jeho modifikace.

Autoregresní model AR(1)

Je-li náhodná složka ε_t determinována bezprostředně předcházející hodnotou ε_t-1, pak je generována autoregresním procesem AR(1)

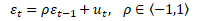ρ ... koeficient autokorelace prvního řádu, u_t ... normálně rozdělená náhodná složka

Je-li parametr ρ = 0, pak náhodná složka vykazuje sériovou nezávislost, ρ = 1 vyjadřuje pozitivní autokorelaci a ρ = -1 negativní autokorelaci.

V praxi neznámý parametr ρ odhadujeme jako výběrový autokorelační koeficient r procesu AR(1) na základě reziduální složky

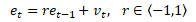
r ... výběrový odhad autokorelačního koeficientu ρ, e_t ... hodnota rezidua v čase t, e_t-1 ... hodnota rezidua v čase t-1

Odhad autokorelačního parametru se provádí standardně pomocí metody nejmenších čtverců. Odhadovou funkcí r získáme na základě parciální derivace minimalizačního kritéria

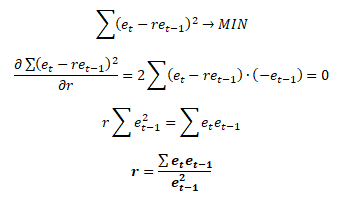
K posouzení statistické (ne)významnosti autokorelačního koeficientu a tím pádem (ne)významnosti autokorelace reziduí je nutné odhadnout kovarianční (rozptylovou) matici odhadové funkce r

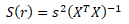
S(r) ... kovarianční matice, s² ... rozptyl reziduální složky, (X^TX)^-1 ... inverzní matice vypočtená z hodnot e_t-1

a rozptyl reziduální složky autoregresního modelu

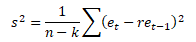
Odmocniny diagonálních prvků kovarianční matice S(r) jsou odhady standardních chyb s(r) regresních parametrů, které se používají k testování statistické významnosti

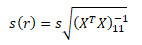
Je třeba upozornit, že matice (X^TX) a tedy i inverzní matice (X^TX)^-1 v autoregresním modelu procesu AR(1) jsou řádu n = 1, tj. jednoprvkové matice.

Odhadnutou standardní chybu odhadu r pak využijeme k testování statistické významnosti pomocí t-testu, který má Studentovo rozdělení t

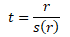
Durbin-Watsonův test

Autokorelace prvního řádu se nejčastěji testuje pomocí Durbin-Watsonova testu, který se označuje jako d nebo DW test. DW test bývá součástí běžných ekonometrických softwarů (např. Gretl).

DW test není použitelný pro regresní modely bez úrovňové konstanty a modely se zpožděnou závisle proměnnou mezi vysvětlujícími proměnnými.

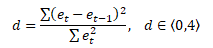
kde e_t je hodnota rezidua v čase t, e_t-1 je hodnota rezidua a v čase t-1

DW statistika má symetrické rozdělení se střední hodnotou E(d) = 2. Hodnoty v její blízkosti představují sériovou nezávislost náhodné složky. Hodnoty blízké 0 představují pozitivní autokorelaci náhodné složky a hodnoty blízké 4 představují negativní autokorelaci.

K přesnému posouzení výsledků testovací statistiky d se používají tabulkové hodnoty, které vymezují intervaly pozitivní a negativní autokorelace, interval nulové autokorelace a intervaly šedé zóny (neprůkaznosti). Dolní d_L a horní d_U meze jsou koncipovány pro počet pozorování n a počet nezávisle proměnných k.

Například pro n=8 a k=1 jsou d_L = 0,76 a d_U = 1,33.

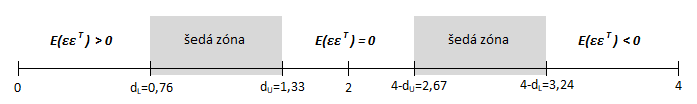
Durbinovo h

Je-li do regresního modelu mezi nezávisle proměnné zahrnuta zpožděná závisle proměnná y_t-1, pak ztrácí statistika d na síle. V takovém případě se pro testování sériové závislosti odhadnuté náhodné složky používá modifikovaný test Durbinovo h.

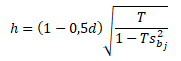
d ... Durbin-Watsonova statistika, T ... počet pozorování, s_bj² ... odhad rozptylu parametru b_j zpožděné závisle proměnné