Kritéria pro volbu regresního modelu vzorce

V rámci regresního modelování můžeme dojít k závěru, že existuje několik vhodných modelů, které vysvětlují závisle proměnnou. Cílem příspěvku je představit několik kritérií, které pomohou vybrat nejvhodnější model z množiny přijatelných modelů.

Představím kritéria, se kterými pracuje ekonometrický software Gretl v rámci odhadu regresního modelu metodou nejmenších čtverců. Vybranými kritérii jsou koeficient determinace R², korigovaný koeficient determinace adjusted R², Akaikovo kritérium AIC a Schwarzovo kritérium SIC. Všechny uvedená kritéria jsou založeny na minimalizaci reziduální složky regresního modelu RSS a penalizaci nadměrného počtu parametrů v modelu.

Reziduální složka modelu RSS

Reziduální součet čtverců RSS je suma čtverců rozdílů jednotlivých empirických hodnot závisle proměnné y a její vyrovnanou hodnotou Y. Reziduální součet čtverců přestavuje minimalizační kritérium metody nejmenších čtverců

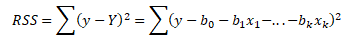
Residuální složka modelu je v různých úpravách použita ve všech následujících informačních kritérií.

Koeficient determinace R²

Kritérium je založeno na rozkladu rozptylu empirických hodnot závisle proměnné TSS na rozptyl vyrovnaných hodnot závisle proměnné ESS a rozptyl residuální složky modelu RSS. Čím nižší je rozptyl residuální složky, tím vyšší je hodnota R². Takový model se jeví jako kvalitní a empirická data se lépe shodují s modelem.

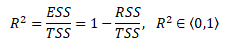
Koeficient determinace je detailnějí rozebrán v kapitole Testování klasického lineárního regresního modelu.

Korigovaný koeficient determinace

Pro výběr nejvhodnějšího modelu je lepší použít upravený koeficient determinace, který zohledňuje počet regresních parametrů k + 1 v modelu a rozsah pozorování.

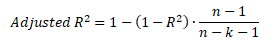
Přičemž platí, že R² ≥ Adjusted R². Korigovaný koeficient determinace penalizuje nadměrný počet regresních parametrů k + 1 v modelu.

Akaikovo kritérium AIC

Penalizace za nadměrný počet regresních parametrů k + 1 v modelu je rozpracována také v rámci Akaikeho informačního kritéria. Akaikeho informační kritérium je součástí ekonometrického softwaru Gretl a vychází z formulace:

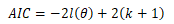
kde l(θ) je logaritmus věrohodnosti, k + 1 je počet parametrů v modelu.

V případě odhadu modelu metodou nejmenších čtverců lze logaritmus věrohodnosti zapsat ve tvaru

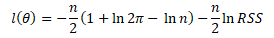
Po substituci logaritmu věrohodnosti do kritéria AIC získáme finální podobu vzorce pro výpočet kritéria

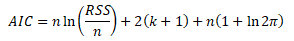
Jednodušší variantu AIC získáme, pokud kritérium vydělíme počtem pozorování n a odečteme konstantu 1 + ln2Π. Jednodušší varianta se stejnou vypovídací schopností má následující tvar

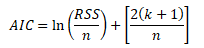
Druhý člen penalizuje počet regresních parametrů v modelu. Kritérium stejně jako Adjusted R² zohledňuje počet regresních parametrů k + 1 a rozsah pozorování n.

Čím nižší je hodnota AIC kritéria, tím nižší je residuální složka modelu. Takový model vykazuje lepší shodu s empirickými hodnotami závisle proměnné.

AIC kritérium se také používá pro rozhodnutí o délce zpoždění v autoregresních model AR(p).

Schwarzovo kritérium SIC

Schwarzovo kritérium je alternativou k AIC, které rovněž penalizuje nadměrný počet regresních parametrů v modelu. Stejně jako všechny ostatní kritéria je součástí softwaru Gretl a má následující tvar

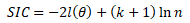
kde l(θ) je logaritmus věrohodnosti, k + 1 je počet parametrů v modelu.

Substitucí logaritmu věrohodnosti do kritéria SIC získáme finální podobu vzorce pro výpočet kritéria

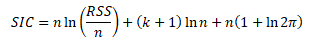
Jednodušší variantu SIC získáme, pokud kritérium vydělíme počtem pozorování n a odečteme konstantu 1 + ln2Π.

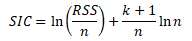
Druhý člen kritéria je penalizační faktor za počet regresních parametrů k + 1.

Stejně jako v případě kritéria AIC platí, že čím nižší je hodnota kritéria SIC, tím lépe se model shoduje s empirickými hodnotami závisle proměnné.