Optimalizace funkce tržeb firmy

Cílem příspěvku je optimalizace funkce tržeb firmy operující v prostředí nedokonalé konkurence. Na základě teoretických dat je odhadnuta mikroekonomická funkce tržeb firmy, která má kvadratický tvar. V modelu vystupují tržby jako závisle proměnná y a množství prodané produkce jako nezávisle proměnná x.

Nedokonale konkurenční trh

Firma prodává své výrobky na nedokonale konkurenčním trhu. To znamená, že má určitou kontrolu nad cenou produkce. Jinými slovy, může zvýšit prodej výrobků snížením ceny. Zda však budou celkové tržby růst nebo klesat závisí na cenové elasticitě poptávky pro produkci firmy. Firmy v odvětví vyrábí diferencovaný produkt, existují překážky vstupu do odvětví a ekonomické subjekty mají k dispozici rozdílnou úroveň informací.

Základní pojmy z mikrokonomie

Celkové tržby představují sumu peněz, které firma získá prodejem svých výrobků a služeb.

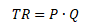
TR ... celkové tržby, P ... cena, Q ... množství prodaných výrobků a služeb

Mezní tržby představují změnu celkových tržeb v důsledku změny prodané produkce o jednotku.

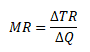
MR ... mezní tržby, Δ ... delta ... symbol pro změnu

Průměrné tržby představují celkové tržby připadající na jednotku prodané produkce.

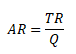
AR ... průměrné tržby

Bodový graf tržeb

Průběh závislosti dvou proměnných můžeme zobrazit graficky, z čehož můžeme zvolit správný tvar regresní funkce. Následující tabulka obsahuje počet pozorování n, objem prodané produkce Q, jednotkovou cenu P a celkové tržby firmy TR.

Vývoj tržeb firmy

n	Q	P	TR
1	0,0	20,0	0,0
2	4,0	19,0	76,0
3	8,0	16,0	128,0
4	10,0	14,0	140,0
5	15,0	13,0	195,0
6	23,0	11,0	253,0
7	32,8	8,0	262,4
8	41,0	7,0	287,0
9	46,0	6,0	276,0
10	68,0	5,0	340,0
11	84,0	4,0	336,0
12	85,0	3,0	285,0
13	100,0	2,0	200,0
14	105,0	1,0	105,0
15	131,0	0,5	65,5
16	135,0	0,1	13,5

Zajímá nás vztah objemu prodané produkce Q a celkových tržeb TR, které jsou dány součinem prodané produkce a ceny. S poklesem ceny dochází k růstu objemu prodané produkce a růstu celkových tržeb firmy. Od určitého bodu však dochází k poklesu celkových tržeb. Z uvedeného průběhu i z bodového grafu lze usoudit, že vývoj celkových tržeb v závislosti na prodaném množství výrobků má parabolický tvar.

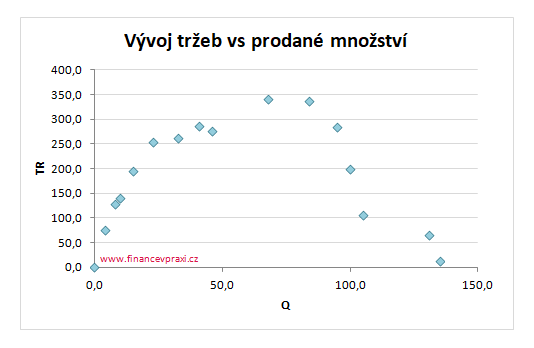
To však není překvapující, neboť z mikroekonomické teorie je známo, že celkové tržby firmy v prostředí nedokonalé konkurence mají tvar paraboly a koeficientem a < 0.

Bodové odhady parametrů modelu

Hledáme bodové odhady b₀, b₁, ..., b_k neznámých parametrů β₀, β₁, ..., β_k parabolické regresní funkce

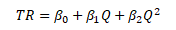
Parametry soustavy normálních rovnic lze odhadnout pomocí Cramerova pravidla nebo bodové odhadové funkce v maticovém vyjádření b = (X^TX)^-1X^Ty. Výsledná parabolická rovnice s bodovými odhady regresních parametrů má následující tvar:

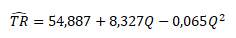
Testování kvality regresního modelu

K testování statistické průkaznosti odhadů regresních parametrů se používá t-test. Vyhodnocení probíhá porovnáním absolutní hodnoty vypočtených t a tabelovaných hodnot, které získáte ze statistických tabulek nebo pomocí excelovské funkce TINV(). Na 5% hladině významnosti vychází tabelovaná hodnota 2,16.

Odhady a verifikace regresních parametrů

Parametr	bj	s(bj)	t	p-value
est β0	54,887	22,122	2,481	0,028
est β1	8,327	9,16	9,09	0,000
est β2	-0,065	0,007	-9,475	0,000

Jelikož vypočtené hodnoty t-testu převyšují tabelované hodnoty můžeme zamítnout nulovou hypotézu H₀ o statistické nevýznamnosti odhadů regresních parametrů ve prospěch alternativní hypotézy H₁ o jejich statistické významnosti.

Hodnota p-value vyjadřuje nejnižší možnou hladinu významnosti, na které ještě lze zamítnout nulovou hypotézu o nevýznamnosti regresních parametrů. Například nulovou hypotézu parametru b₀ lze zamítnout ještě na 2,8% hladině významnosti. Hodnoty p-value vypočítáte například pomocí excelovské funkce TDIST().

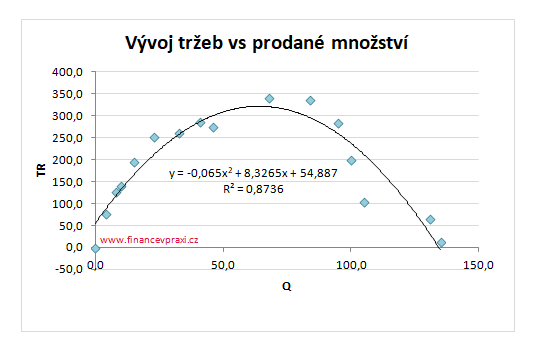
Koeficient determinace říká, že se nám pomocí modelu podařilo vysvětlit 87,36 % variability celkových tržeb.

Testování reziduální složky

Autokorelace reziduální složky je nejčastěji testována na základě Durbin-Watsonovy statistiky označované jako d. Pro přesné posouzení autokorelace zařadíme vypočtenou hodnotu d do intervalu pozitivní autokorelace, nulové autokorelace, negativní autokorelace nebo šedé zóny. Uvedené intervaly jsou vymezeny tabelovanými hodnotami d_L a d_U, které získáte ze statistických tabulek.

Na 5% hladině významnosti jsou pro n = 16 a k = 2 základní tabelované hodnoty pro šedou zónu d_L = 0,98 a d_U = 1,54.

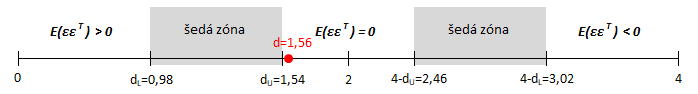
Na základě vypočtené statistiky d = 1,562 můžeme vyloučit autokorelaci reziduální složky, neboť se nachází v intervalu nulové autokorelace.

Maximalizace celkových tržeb

Z odhadnutého modelu celkových tržeb můžeme nyní vypočítat optimální množství prodané produkce, při kterém jsou maximalizovány celkové tržby.

První derivací odhadnuté funkce celkový tržeb získáme funkci mezních tržeb, ze které dopočítáme Q maximalizující tržby

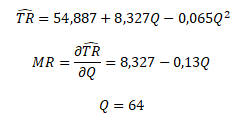
Maximální úrovně celkových tržeb ve výši 322 peněžních jednotek je dosaženo při prodeji 64 jednotek produkce s cenou 5 peněžních jednotek za kus.

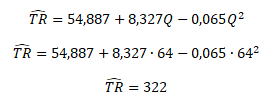
Úprava regresního modelu

Z odhadnutého regresního modelu vyplývá, že při nulovém prodeji produkce firma vydělá 54,9 peněžních jednotek. To nedává smysl a je potřeba upravit tvar regresní funkce. Odhadneme kvadratickou funkci bez úrovňové konstanty, tj. b₀ = 0. Graf paraboly nyní bude procházet počátkem.

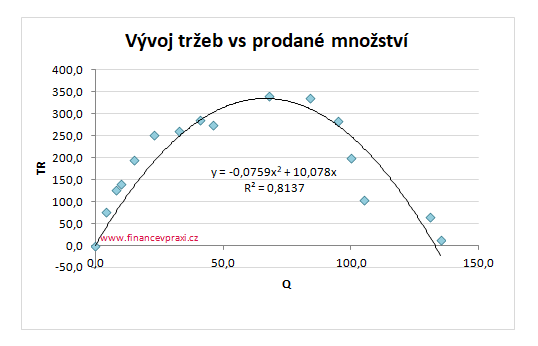
První derivací regresního modelu bez úrovňové konstanty vypočteme mezní tržby a vyjádříme Q

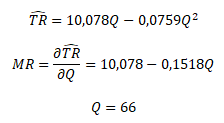
Firma maximalizuje tržby při objemu prodeje Q = 66 a zaokrouhlené ceně P = 5.

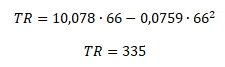
Odhad kvadratické regrese bez úrovňové konstanty má sice nižší koeficient determinace R², avšak lépe vyhovuje z hlediska logiky.