Testování regresního modelu

Odhadnutý regresní model je třeba statisticky ověřit hned z několika hledisek. Testují se dílčí parametry modelu (t-test), model jako celek (koeficient determinace a F-test) a testy zaměřené reziduální složku (sériová nezávislost, konstantní rozptyl a normalita). Je-li statistická verifikace úspěšná, lze teprve pak výsledky vztáhnout na celou populaci a použít pro předpovědi budoucích hodnot.

Cílem příspěvku je popsat základní statistické metody pro testování dílčích parametrů modelu a modelu jako celku.

Normalita modelu a odhad standardní chyby

Pro testování hypotéz a konstrukci intervalů spolehlivosti se předpokládá normální rozdělení náhodné složky. Od rozdělení náhodné složky se odvíjí rozdělení odhadů b neznámých parametrů β.

Ke klasickým předpokladům lineárního regresního modelu se přidává předpoklad normality náhodné složky. Předpoklad říká, že vektor náhodné složky ε má mít normální rozdělení s nulovou střední hodnotou a kovarianční maticí ∑ = σ²I_n.

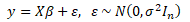
Odhadová funkce b = (X^TX)^-1X^Ty s normálním rozdělením má střední hodnotou β a kovarianční matici σ²(X^TX)^-1

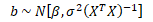
Hodnoty rozptylu náhodné složky σ² v kovarianční matici jsou neznámé. Proto je nutné při praktickém testování modelu nahradit neznámý rozptyl σ² jeho odhadem s²

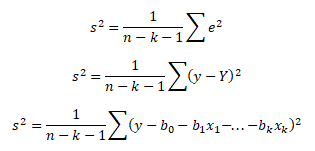
y ... skutečná hodnota závisle proměnné, Y ... výběrová regresní funkce, n ... počet pozorování, k + 1 ... počet regresních parametrů v modelu včetně úrovňové konstanty

Na základě odhadu s² pak můžeme neznámou kovarianční matici V(b) nahradit jejím odhadem S(b)

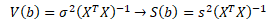
Odmocniny diagonálních prvků kovarianční matice jsou odhady standardních chyb regresních parametrů s(b_j). Standardní chyby regresních parametrů vyjadřují míru přesnosti bodové odhadové funkce b. V rámci statistické verifikace odhadů se používají k testování statistické významnosti regresních parametrů a oprávněnosti být v modelu.

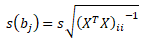
Testování regresních parametrů modelu

K testování statistické významnosti odhadnutých regresních parametrů se používá t-test, který je založen na Studentově rozdělení t s n - (k + 1) stupni volnosti. Testovací kritérium poměřuje odhady jednotlivých parametrů a jejich standardních chyb

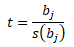
Testovací kritérium je vyhodnocováno porovnáním absolutní hodnoty vypočtené statistiky |t| s tabelovanou hodnotnou kvantilu t_1-α/2[n - (k + 1)] na zvolené hladině významnosti α s n - (k + 1) stupni volnosti.

Jestliže je |t| větší než tabelovaná hodnota, zamítáme nulovou hypotézu H₀ o statistické nevýznamnosti parametru v modelu ve prospěch alternativní hypotézy H₁ o statistické významnosti.

Vyhodnocení testu probíhá následujícím způsobem

|t| > t_1-α/2(n - k - 1) ⇒ proměnná má vliv na vysvětlovanou proměnnou
|t| < t_1-α/2(n - k - 1) ⇒ proměnná nemá vliv na vysvětlovanou proměnnou

Kvalita regresního modelu

Kvalita regresního modelu se ověřuje pomocí koeficientu determinace, který se označuje R²

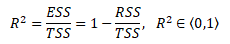
Je založen na rozkladu rozptylu empirických hodnot závisle proměnné (TSS) na rozptyl vyrovnaných hodnot závisle proměnné (ESS) a rozptyl reziduální složky modelu (RSS)

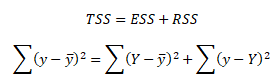
TSS = ∑(y_i - y)² ... rozptyl empirických hodnot závisle proměnné, ESS = ∑(Y_i - y)² ... rozptyl vyrovnaných hodnot závisle proměnné, RSS = ∑(y_i - Y_i)² ... rozptyl residuální složky

Reziduální součet čtverců odchylek je minimalizační kritérium metody nejmenších čtverců. Čím nižší je rozptyl reziduální složky, tím kvalitnější je odhadnutý model a empirická data se shodují s modelem.

V praxi se doporučuje použít i takzvaný korigovaný koeficient determinace, který zohledňuje počet regresních parametrů v modelu a rozsah pozorování

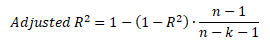
Přičemž platí, že R² ≥ adjusted R². Korigovaný koeficient determinace penalizuje nadměrný počet parametrů k + 1 v modelu.

Testování významnosti modelu

Pro testování statistické významnosti regresního modelu se používá F-test, který je založen na koeficientu determinace.

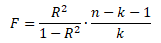
Testovací kritérium má Fisherovo-Snedecorovo rozdělení F s počtem regresních parametrů k a n - k - 1 stupni volnosti.

Jestliže je kalkulovaná hodnota F-testu větší než tabulková hodnota kvantilu F_{1 - α}(k, n - k - 1), zamítáme nulovou hypotézu H₀ o statistické nevýznamnosti modelu ve prospěch alternativní hypotézy H₁ o statistické významnosti modelu a shodě modelu s daty.

F > F_{1 - α}(k, n - k - 1) ⇒ model je statisticky významný
F < F_{1 - α}(k, n - k - 1) ⇒ model je statisticky nevýznamný