Koeficienty kovariance a korelace
Publikováno: 19.5.2017

Lineární závislost veličin, koeficient kovariance a korelace, kovarianční a korelační matice
- kovariance
- korelace
- jednotková matice
Kovariance a korelace vyjadřují míru vzájemné závislosti veličin/proměnných. Používají se například v regresní analýze ke kvantifikaci vzájemné závislosti proměnných, kvality regresního modelu a výpočtu koeficientu beta cenných papírů. Ve finanční teorii májí široké uplatnění zejména v moderní teorii portfolia cenných papírů.
Kovariance
Kovariance C(X,Y) je statistická charakteristika, která určuje vzájemnou závislost veličin X a Y. Je definována jako střední hodnota součinu odchylek veličin X a Y od jejich středních hodnot
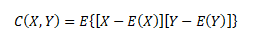
E(X), E(Y) ... střední hodnoty veličin
Kovariance může nabývat hodnot na intervalu ⟨-∞,+∞⟩. Na základě vypočtené kovariance můžeme posoudit vzájemnou závislost následujícím způsobem:
- C(X,Y) > 0 - veličiny X a Y se pohybují stejným směrem (současně rostou nebo klesají)
- C(X,Y) = 0 - veličiny X a Y jsou navzájem nezávislé
- C(X,Y) < 0 - mezi veličinami X a Y je inverzní vztah (jedna roste a druhá klesá a naopak)
V praxi rozlišujeme kovarianci základního souboru (populace) σxy
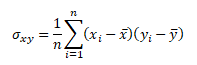
σxy ... populační koeficient kovariance, sxy ... výběrový koeficient kovariance (n < 30), x, y... prosté aritmetické průměry veličin X a Y n ... počet pozorování
a výběrovou kovarianci sxy, která se používá pro odhad populační kovariance při malém rozsahu dat (n < 30)
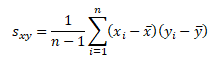
Při zjišťování závislosti mezi více než 2 veličinami jsou jednotlivé párové kovariance uspořádány do kovarianční matice C. Kovarianční matice je symetrická matice s diagonálními prvky rovny rozptylu jednotlivých veličin. Prvky mimo diagonálu představují párové koeficienty kovariance.
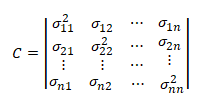
Důkaz rovnosti kovariance σ11 na diagonále kovarianční matice a rozptylu σ2 pro vybranou proměnnou x1 je následující
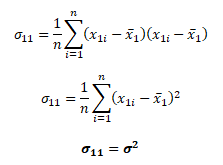
Korelační koeficient
Korelace ρ(X,Y) měří lineární závislost mezi veličinami X a Y. Korelační koeficient standardizuje kovarianci a výsledkem jsou hodnoty na intervalu ⟨-1; 1⟩. Korelace je vyjádřena jako poměr kovariance k součinu směrodatných odchylek veličin X a Y.
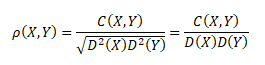
D2(X), D2(Y) ... rozptyly náhodných veličin X a Y, D(X), D(Y) ... směrodatné odchylky náhodných veličin X a Y
Význam výsledných hodnot koeficientů korelace:
- ρ(X,Y) = 1 - mezi veličinami X a Y existuje dokonalá přímá závislost
- ρ(X,Y) = 0 - veličiny X a Y nejsou korelované
- ρ(X,Y) = -1 - mezi veličinami X a Y je dokonalý inverzní vztah
Základní koeficient korelace, který měří lineární závislost mezi 2 proměnnými, se nazývá párový korelační koeficient. Rozlišujeme koeficient korelace základního souboru (populace) ρx,y
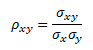
σxy ... kovariance veličin X a Y, σx, σy ... směrodatné odchylky veličin X a Y
a výběrovou korelaci rx,y, která se používá jako odhad korelace základního souboru v případě malého rozsahu dat (n < 30)
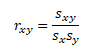
sxy ... výběrová kovariance veličin X a Y, sx, sy ... výběrové směrodatné odchylky veličin X a Y (n < 30)
V případě zkoumání lineární závislosti mezi více než 2 proměnnými jsou párové korelační koeficienty uspořádány do korelační matice (ρ). Korelační matice je symetrická matice s diagonálními prvky rovny 1. Prvky mimo diagonálu představují párové koeficienty korelace.
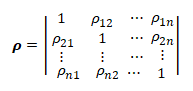
Jestliže jsou korelační koeficienty mimo diagonálu nulové je korelační matice rovna jednotkové matici (I). Důkaz rovnosti korelačního koeficientu ρ11 na diagonále korelační matice a 1 pro vybranou proměnnou x1 je následující
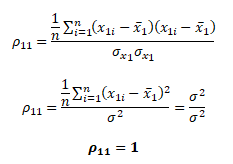
Funkce v MS Excel
- COVAR() - vrátí hodnotu kovariance základního souboru (2003)
- COVARIINACE.P() - vrátí hodnotu kovariance základního souboru (> 2003)
- COVARIANCE.S() - vrátí hodnotu kovariance výběru (> 2003)
- CORREL() - vrátí párový korelační koeficient
- CYHELSKÝ, L., KAHOUNOVÁ, J., HINDLS, R.: Elementární statistická analýza. Management Press 2001, Praha. Druhé doplněné vydání, 319 stran. ISBN 80-7261-003-1
- ČÁMSKÝ, F.: Teorie portfolia. Masarykova univerzita 2007, Brno. Druhé přepracované a rozšířené vydání, 123 stran. ISBN 978-80-210-4252-0
- HINDLS, R., HRONOVÁ, S., SEGER, J., FISCHER, J.: Statistika pro ekonomy. Profesional publishing 2007, Praha. Osmé vydání, 415 stran. ISBN 978-80-86946-43-6
- MINAŘÍK, B.: Statistika II. Mendelova zemědělská a lesnická univerzita v Brně 2007, Brno. První vydání, 136 stran. ISBN 978-80-7375-033-6
- Wikipedie. Kovariance [on-line] [cit. 2017-05-19]. Dostupné z WWW: https://cs.wikipedia.org/wiki/Kovariance
- Wikipedie. Korelace [on-line] [cit. 2017-05-19]. Dostupné z WWW: https://cs.wikipedia.org/wiki/Korelace

