Elasticita poptávky v příkladech
Publikováno: 15.12.2017
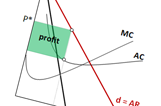
Výpočet cenové elasticity poptávky, ceny maximalizující výdaje spotřebitele a tržby firem, křížové a důchodové elasticita poptávky.
- cenová elasticita
- maximalizace tržeb
- důchodová elasticita
Vzorce pro řešení příkladů a teorii poptávky najdete v předchozí kapitole Křivka poptávky a elasticita poptávky. Následují příklady, které se týkají:
- Příklad 1 - cenová elasticita poptávky
- Příklad 2 - křižová elasticita poptávky
- Příklad 3 - cena maximalizující spotřební výdaje
- Příklad 4 - cenová elasticita poptávky a grafické zobrazení poptávky
- Příklad 5 - důchodová elasticita poptávky
Příklad 1
Koeficient cenové elasticity poptávky je -3, přičemž poptávané množství se zvýšilo o 30 %. O kolik procent se musela změnit cena?
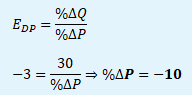
Mezi cenou a poptávaným množstvím je inverzní vztah. Proto je koeficient cenové elasticity poptávky záporný. 10% snížení ceny vyvolalo růst poptávky o 30 %. Poptávka po daném statku je elastická.
Příklad 2
Koeficient křížové elasticity poptávky je -2, přičemž poptávané množství statku X (QX) se snížilo o 20 %. O kolik procent se musela změnit cena statku Y (PY) a o jaké statky se jedná?
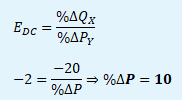
20% pokles poptávky po statku X byl způsoben růstem ceny statku Y o 10 %. Statky se ve spotřebě doplňují, proto růst ceny jednoho statku způsobí pokles prodejů statku druhého. Statky jsou komplementy.
Příklad 3
Při jaké ceně jsou maximalizovány výdaje spotřebitele na koupi daného statku. Individuální poptávka spotřebitele je popsána funkcí Q = 80 - 4P?
Výdaje spotřebitele jsou maximalizovány při jednotkové cenové elasticitě poptávky. Proto je EDP rovno -1.
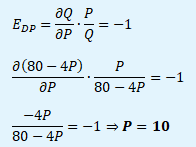
Výdaje spotřebitele na koupi statku jsou maximalizovány při ceně P = 10.
Příklad 4
Je dána tržní poptávka Q = 160 - 4P. Úkolem je spočítat cenovou elasticitu poptávky (EDP) pro dané ceny, identifikovat charakter poptávky a zobrazit výsledky graficky.
Při jaké ceně firmy maximalizují tržby na daném trhu?
a) EDP pro P = 10?
b) EDP pro P = 20?
c) EDP pro P = 30?
d) při jaké ceně dosahuje firma maximálních tržeb?
Průsečíky poptávky s osou x a y
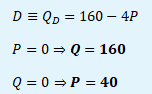
Ad a) P = 10
![Neelastická poptávka v bodě D[160;10] Neelastická poptávka v bodě D[160;10]](../img/ekonomie/mikroekonomie/elasticita-poptavky-priklad-4a.png)
Poptávka je v bodě D[120;10] neelastická.
Ad b) P = 20
![Jednotkově elastická poptávka v bodě D[80;20] Jednotkově elastická poptávka v bodě D[80;20]](../img/ekonomie/mikroekonomie/elasticita-poptavky-priklad-4b.png)
Poptávka je v bodě D[80;20] jednotkově elastická.
Ad c) P = 30
![Elastická poptávka v bodě D[40;30] Elastická poptávka v bodě D[40;30]](../img/ekonomie/mikroekonomie/elasticita-poptavky-priklad-4c.png)
Poptávka je v bodě D[40;30] elastická.
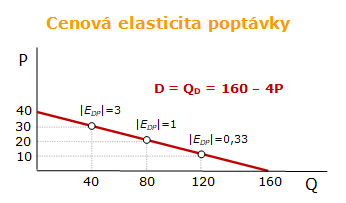
Z uvedeného vyplývá, že se cenová elasticita poptávky v průběhu poptávkové křivky mění. Maximálních spotřebních výdajů je dosaženo při jednotkové elasticitě poptávky, tj. P·Q = 20·80 =1 600 Kč.
Ad d) maximalizace tržeb firem při P = ?
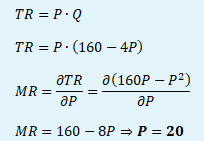
Tržby firem (TR) jsou maximalizovány v bodě jednotkové elasticity poptávky, tj. při ceně 20. K výsledku jsme mohli dojít logickou úvahou nebo početně skrze mezní tržby firem (MR).
Příklad 5
Je dána individuální poptávka spotřebitele po statku X: QX = 50 - 3·PX + 2·PY + 0,03·I. Jaká je důchodová elasticita poptávky (EDI) a charakter daného statku při PX = 8, PY = 10, I = 1000?
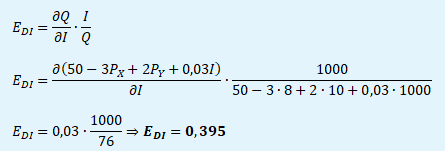
Statek X je normální statek nezbytného charakteru, neboť růst důchodu o 1 % způsobí růst statku X o 0,4 %.

