Tržní rovnováha příklady
Publikováno: 19.11.2018
Výpočet tržní rovnováhy krok za krokem, interakce lineární a kvadratické funkce poptávky s lineární funkcí nabídky
- poptávka
- nabídky
- tržní rovnováha
Příklady navážeme na předchozí teoretickou část tržní rovnováhy a tržního mechanismu. Cílem kapitoly je výpočet rovnovážné ceny a rovnovážného množství na trhu daného statku, výpočet poptávaného množství spotřebiteli a nabízeného množství výrobci při nerovnovážné ceně.
Příklad 1
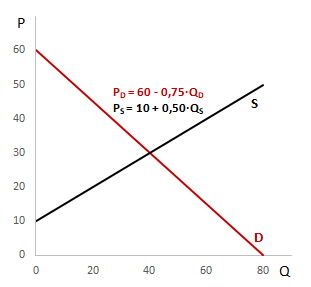
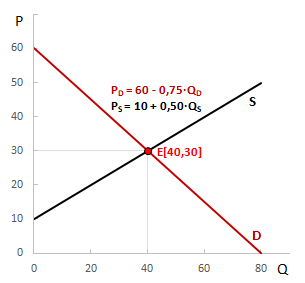
Úkolem je vypočítat rovnováhu trhu, tj. rovnovážnou cenu statku PE a rovnovážné množství QE, a sestavit graf tržní rovnováhy. Jsou dány následující lineární funkce poptávky a nabídky
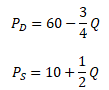
Prvním krokem je výpočet průsečíků křivek s horizontální osou Q a vertikální osou P. Zajímá nás pouze první kvadrant. Jiné kvadranty nedávají ekonomický smysl, neboť obsahují záporné hodnoty.
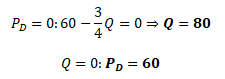
Křivka poptávky protíná osu Q v bodě 80 a osu P v bodě 60. Bod P = 60 představuje cenu, při které spotřebitelé nekoupí žádný statek a opouští trh. Bod Q = 80 představuje maximální množství, které by spotřebitelé požadovali k uspokojení potřeb při nulové ceně, tj. bod nasycení.
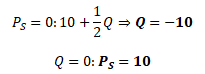
Křivka nabídky protíná osu P v bodě 10, při které výrobci nejsou ochotni vyrábět žádný statek. Sklon křivky nabídky 0,5 je dán hodnotou parametru d.
Z rovnováhy poptávkové ceny PD a nabídkové ceny PS vypočteme rovnovážné množství statku QE
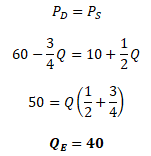
Kompromis mezi spotřebiteli a výrobci se nachází v bodě Q = 40. Dosazením rovnovážného množství do funkcí poptávky a nabídky získáme rovnovážnou cenu PE = 30.
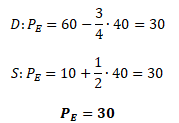
Stejné výsledky PD a PS slouží také jako kontrola správnosti výpočtů.
Příklad 2
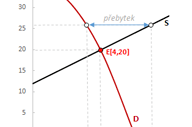
Úkolem je zjistit, jaká situace na trhu nastane při ceně 26 Kč za statek, vypočítat rovnovážnou cenu a rovnovážné množství statku při zadané kvadratické funkci poptávky a lineární funkci nabídky.
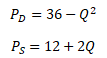
Prvním krokem řešení je výpočet průsečíků křivek s osami Q a P.
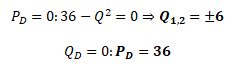
Průsečík poptávky s osou P je v bodě [0,36], který představuje maximální cenu. Na ose Q je to bod [6,0], který představuje maximální množství.
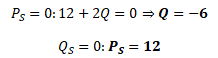
Křivka nabídky má průsečík s osou P v bodě [0,12]. Slovy mikroekonomie představuje tento bod cenu, při které výrobci nejsou ochotni vyrábět statky. Bod Q = -6 neuvažujeme, neboť se nachází mimo první kvadrant, ale je důležitý pro načrtnutí sklonu křivky nabídky.
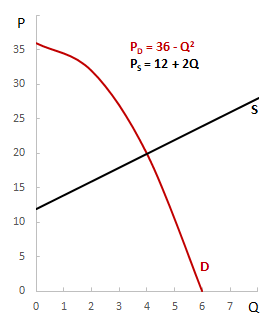
Jaké množství statku by poptávali spotřebitelé a nabízeli výrobci při ceně P = 26?
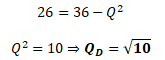
Spotřebitelé by při ceně 26 Kč poptávali množství statku QD = √10, což přibližně odpovídá 3 kusům.
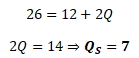
Výrobci by si při této ceně přáli vyrábět a nabízet množství QS = 7. Za dané situace vzniká na trhu přebytek nabídky nad poptávkou. Chtějí-li výrobci prodat svojí produkci, musí snížit cenu.
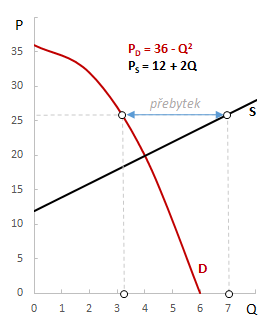
Výpočet rovnovážného množství statku QE vypočteme na základě rovnováhy PD a PS. Rovnovážné množství získáme řešením kvadratické rovnice, přičemž ekonomický smysl dává pouze kladná hodnota.
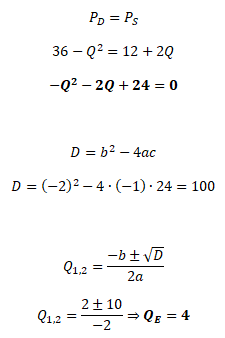
Rovnovážnou cenu PE získáme už pouhým dosazením QE do funkce poptávky nebo funkce nabídky
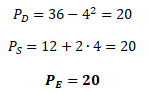
Průsečík křivek poptávky a nabídky se nachází v bodě [4, 20]. Jinými slovy, v průsečíku křivek se nachází tržní rovnováha při rovnovážné ceně 20 Kč a rovnovážném množství 4.