Význam a výpočet reálné úrokové sazby

Reálná úroková sazba je důležitý indikátor střadatele a investora, který informuje o reálném zhodnocení prostředků a změny kupní síly.

Reálná úroková sazba je rovna nominální (peněžní) úrokové sazbě očištěné o očekávanou (ex ante) nebo skutečnou (ex post) míru inflace. Vztah mezi nominální a reálnou úrokovou sazbou definuje Fisherova rovnice

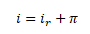
i ... nominální úroková sazba, i_r ... reálná úroková sazba, Π ... sazba inflace

Nominální versus reálná úroková sazba

Pro výpočet skutečného výnosu z investice a bankovního depozita je třeba pracovat s reálnou úrokovou sazbou. Nominální úroková sazba vnáší do výpočtů zkreslení v důsledku inflace. Inflace snižuje kupní sílu peněz a zkresluje dosažené zhodnocení.

Nominální úroková sazba měří výnos v korunách na jednotku investované koruny za určité časové období (nejčastěji rok).

Naopak reálná úroková sazba měří výnosy z investovaného kapitálu ve formě statků a služeb místo peněžních jednotek. Reálná úroková sazba představuje úrok, který udává, kolik statků a služeb si reálně můžeme koupit.

Vysoké nominální úrokové sazby v ekonomice nemusejí nutně znamenat vysoké reálné úrokové výnosy či náklady. Vysoké úrokové sazby mohou být doprovázeny vysokou mírou inflace.

Vzorce pro výpočet reálné úrokové sazby

Vzorec pro výpočet reálné úrokové sazby získáme ze vzorců pro výpočet reálného zhodnocení kapitálu.

První vzorec počítá budoucí reálnou hodnotu investovaného kapitálu (FV) úročením počátečního kapitálu (PV) nominální úrokovou sazbou (i) a diskontováním mírou inflace

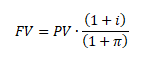
Druhým způsobem je úročení počátečního kapitálu přímo reálnou úrokovou sazbou

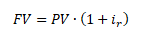
Oba uvedené vzorce vedou ke stejnému výsledku. Jejich vzájemnou úpravou získáme vzorec pro výpočet reálné úrokové sazby i_r

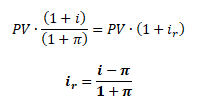
Při nízké míře inflace lze pro odhad reálné úrokové sazby použít výše uvedenou Fisherovu rovnici, ze které vyjádříme i_r.

Reální úroková sazba #1

Jaká je reálná úroková sazba, pokud banka nabízí na jednoleté depozitum roční nominální úrokovou sazbu 8 % a skutečná roční míra inflace je 3 %.

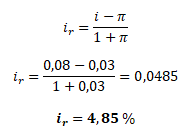
Pokud by klient banky uložil na roční termínový vklad 1 spotřební koš v hodnotě 1000 Kč, po roce by jeho reálná kupní síla vzrostla o 4,85 %. Klient by si koupil více než 1 spotřební koš, tj. 1,049 spotřebního koše (= 1049/1000).

Reální úroková sazba #2

Jaká je reálná úroková sazba, pokud banka nabízí na jednoleté depozitum roční nominální úrokovou sazbu 8 % a skutečná roční míra inflace je 10 %.

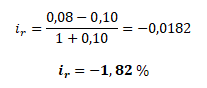
Reálná kupní síla klienta by byla po roce nižší. Mohl by si totiž koupit méně než 1 spotřební koš, tj. 0,982 spotřebního koše (= 982/1000).

Závěr

Kladná reálná úroková sazba představuje reálné zhodnocení uložených prostředků a růst kupní síly. Naopak záporná reálná úroková sazba představuje reálné znehodnocení uložených prostředků a pokles kupní síly.