Model CAPM a koeficient beta příklady

Vzorce pro řešení následujících příkladů včetně teoretických základů koeficientu beta a modelu CAPM najdete v předchozích kapitolách.

Beta a model CAPM v praxi

Na akciové burze je obchodováno 5 společností. Bezrizikové aktivum vynáší 4 % ročně (σ_f = 0 %) a očekávaná výnosnost akciového trhu je 8 % (σ_M = 9,6 %). Úkolem analytika je na základě očekávaných výnosností zjistit ocenění akcií a doporučit investorům akcie vhodné k nákupu. Analytik postupuje následujícími dílčími kroky:

1) výpočte β_i akcií na základě znalosti kovariance s trhem (σ_iM)
2) výpočte β_i akcií na základě znalosti korelace s trhem (ρ_iM)
3) výpočte očekávané rovnovážné výnosnosti akcií [E(r_i)]
4) sestaví přímku SML
5) výpočte α_i akcií a poskytne investiční doporučení klientům investiční společnosti

Výpočty jsou založeny na daných číselných charakteristikách akcií v následující tabulce - skutečná výnosnost akcií (r_i), směrodatná odchylka (σ_i) a kovariance akcie s trhem (σ_iM)

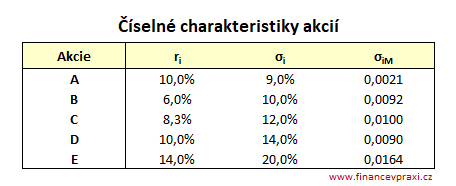
Ad 1) kovarianční verze bety

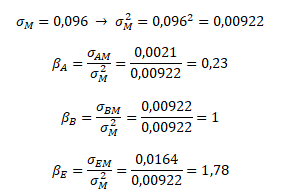
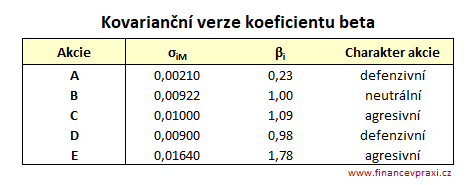
Následující tabulka obsahuje vypočtenou betu pro všech 5 akciových titulů.

Ad 2) korelační verze bety

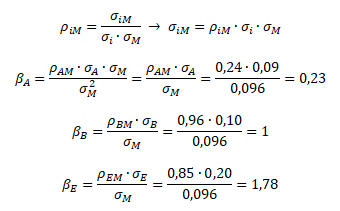
Pomocí korelační verze bety jsme logicky dospěli ke stejným výsledkům jako v předchozím případě. Nezávisí tedy na vybrané metodě výpočtu.

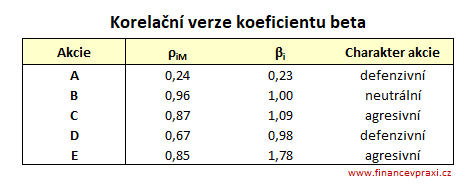
Ad 3) výpočet rovnovážné výnosnosti akcií E(r_i)

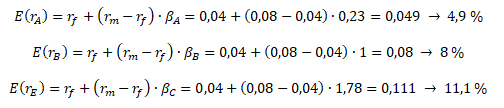
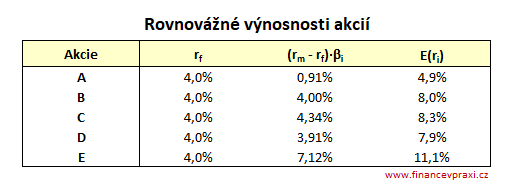
Ad 4) přímka SML

Přímka SML je dána průsečíky bodů [β_f, r_f] a [β_m, r_m]. Lze jí sestavit v MS Excelu pomocí bodového grafu a přidáním lineárního trendu. Lineární trend je prodloužen o 1,5 periody vpřed a zaškrtnuta možnost zobrazení lineární rovnice.

Body na přímce SML přestavují správně oceněné akcie, body nad přímkou představují podhodnocené akcie a body pod přímkou představují nadhodnocené akcie.

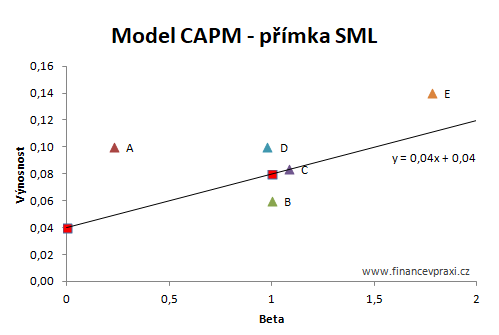
Ad 5) alfa a investiční doporučení

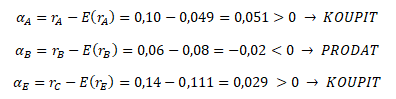
V rámci teorie modelu CAPM by analytik doporučil k nákupu akcie A, E a D. Naopak akcii B by doporučil prodat a akcii C dále držet v investičním portfoliu.