Jednoduché a složené úročení

Jednoduché a složené úročení jsou pilíře, na kterých stojí finanční matematika. Setkáme s nimi u jednoduchých výpočtů typu zhodnocení investovaného kapitálu až po oceňování dluhopisů, akcií a celých společností.

Jednoduché úročení je způsob úročení, kdy jsou úroky počítány pouze z investovaného kapitálu

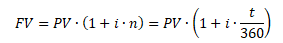
Naopak při použití složeného úročení jsou úroky počítány z investovaného kapitálu a navíc z připsaných úroků za předchozí úrokové období

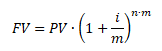
PV ... současná hodnota kapitálu, FV ... budoucí hodnota kapitálu, i ... roční úroková sazba, n ... doba splatnosti (pro jednoduché úročení n = t/360), m ... počet úrokových období za 1 rok (frenkvence úročení)

Okamžik připsání úroků

Podle okamžiku připsání úroků se můžete setkat s termínem polhůtní úročení, při kterém jsou úroky počítány ze současné hodnoty a připisují se na konci úrokového období.

Anebo s předlhůtním úročením, kdy jsou úroky počítány z budoucí hodnoty a připisují se na počátku úrokového období (typické pro eskont směnky).

V následujícím textu je uvažováno pouze polhůtní úročení, které je v praxi běžnější.

Časová hodnota peněz

Současná a budoucí hodnota kapitálu souvisí s časovou hodnotou peněz. Vychází z předpokladu, že jedna koruna dnes má vyšší kupní sílu než jedna koruna v budoucnu. Pokud se tedy investor vzdá své současné spotřeby a peníze investuje náleží mu odměna, která pokles kupní síly kompenzuje. Rozdíl mezi současnou a budoucí hodnotou kapitálu se nazývá úrok.

Úrok by měl zohledňovat znehodnocení peněz v důsledku inflace a rizikové přiřážky stanovených na základě rizikovosti investice.

Jednoduché a složené úročení

Rozdíl mezi jednoduchým a složeným úročením nejlépe pochopíte na následujícím příkladě. Klient banky disponuje volnými peněžními prostředky ve výši 1 000 Kč, které by rád uložil v bance. Banka nabízí termínový účet s dobou splatnosti 4 roky a roční úrokovou sazbou 20 %. Úroky jsou připisovány ročně. Zdanění úrokových výnosů není uvažováno.

Výpočet budoucí hodnoty vkladu

Jednoduché úročení	Složené úročení	Rozdíl
FV0 = 1 000	FV0 = 1 000
FV1 = 1 000 · (1 + 0,20 · 1) = 1 200	FV1 = 1 000 · (1 + 0,20)1 = 1 200	0
FV2 = 1 000 · (1 + 0,20 · 2) = 1 400	FV2 = 1 000 · (1 + 0,20)2 = 1 440	-40
FV3 = 1 000 · (1 + 0,20 · 3) = 1 600	FV3 = 1 000 · (1 + 0,20)3 = 1 728	-128
FV4 = 1 000 · (1 + 0,20 · 4) = 1 800	FV4 = 1 000 · (1 + 0,20)4 = 2 074	-274

Pokud bychom u banky uložili částku 1.000 Kč na jeden rok s ročním úrokovým obdobím, získali bychom v obou způsobech úročení stejné zhodnocení ve výši 200 Kč.

Pokud bychom uložili 1.000 Kč na dva roky s ročním úrokovým obdobím, získali bychom v případě jednoduchého úročení každý rok 200 Kč, tj. celkem 400 Kč. Ale v případě složeného úročení bychom získali 1.440 Kč, tj. o 40 Kč více. Důvodem je skutečnost, že v případě složeného úročení se úroky počítají i z připsaných úroků na účet, tj. z částky 1.200 Kč po prvním roce.

Analogickým způsobem bychom postupovali i ve třetím a čtvrtém roce úročení.

Z následujícího obrázku i předešlého výpočtu by mělo být patrné, že úroky u složeného úročení rostou exponenciálně, zatímco co u jednoduchého úročení lineárně.

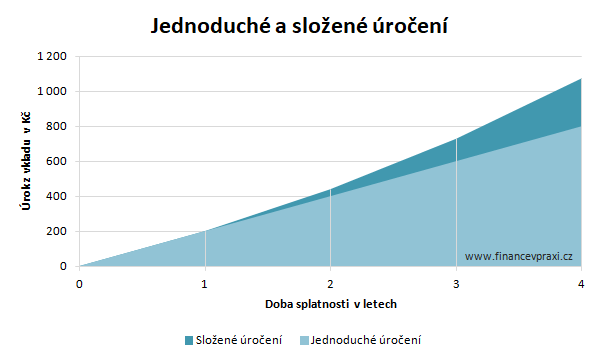
Současná hodnota kapitálu

Dosud jsme uvažovali základní vztahy jednoduchého a složeného úročení pro výpočet budoucí hodnoty kapitálu. Uvedené vztahy fungují i opačným směrem, tj. v případech, kdy chceme přepočítat budoucí hodnotu kapitálu na současnou hodnotu.

Vyjádřením současné hodnoty PV z obou vzorců získáme pro jednoduché úročení vztah

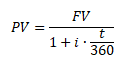
a složené úročení

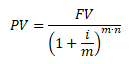
Typickým příkladem je, kolik bychom dnes měli uložit v bance při daných parametrech úročení, jestliže v budoucnu budeme potřebovat určitou konkrétní částku na úhradu dluhu či nákup spotřební věci apod.

Převod budoucí hodnoty kapitálu na současnou se označuje jako diskontování, které se například používá pro hodnocení investic pomocí metody Čisté současné hodnoty.