Logaritmická funkce a výpočet logaritmu

Logaritmická funkce je dána předpisem

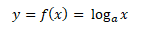
kde y je závisle proměnná, a je základ logaritmu a x je nezávisle proměnná. Předpis logaritmické funkce se čte jako logaritmus čísla x o základu a. Základ logaritmu a musí být větší než nula a zároveň různý od jedné

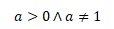
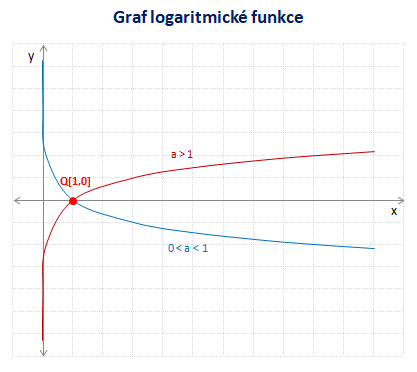
Grafem logaritmické funkce je logaritmická křivka. Graf logaritmické funkce prochází bodem Q[1,0]. Pro základ a > 1 je křivka rostoucí a pro 0 < a < 1 je klesající.

Logaritmická funkce je inverzní funkcí k exponenciální funkci, proto musí platí následující ekvivalence

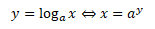
Definiční obor logaritmické funkce je ohraničen nulou a plus nekonečném, přičemž oborem funkčních hodnot je množina všech reálných čísel

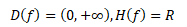
Z následujícího grafu je patrné, že definičním oborem exponenciální funkce y = a^x je množina všech reálných čísel a obor funkčních hodnot je omezen nulou a plus nekonečném. Je to přesně naopak než u logaritmické funkce. To je dáno tím, že se jedná o inverzní funkce.

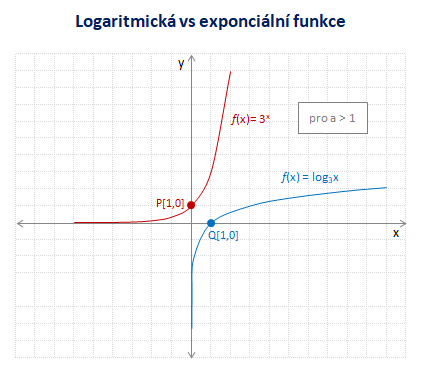
Logaritmická funkce je ryze monotónní funkce, neboť je rostoucí nebo klesající v celém definičním oboru. Funkce není omezená shora ani zdola, a nemá maximum ani minimum.

Vzorce a věty o logaritmech

Pro výpočet logaritmů se používají následující definiční vztahy a věty o logaritmech

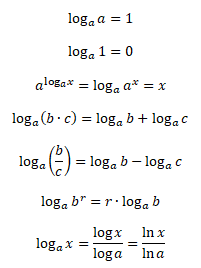
První tři příklady vycházejí z ekvivalentního vztahu logaritmické a exponenciální funkce. Na dalších příkladech jsou demonstrovány věty o logaritmech.

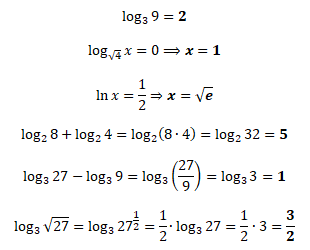
Speciální druhy logaritmů

Logaritmus o základu 10 se nazývá desítkový nebo dekadický logaritmus a zapisuje se jako log x.

Logaritmus o základu e se nazývá přirozený logaritmus a označuje se jako ln x. Základem přirozeného logaritmu je Eulerova konstanta, která je přibližně rovna 2,71828. Právě přirozený logaritmus se velmi často používá v ekonomii a finanční teorii.

Dalším typem logaritmu je binární logaritmus o základu 2, který se používá v informatice.

Aplikace přirozeného logaritmu

Přirozený logaritmus se používá například v analýze časových řad k aproximaxi malých relativních změn sledované veličiny. Relativní změnu ceny P_t finančního aktiva můžeme vyjádřit

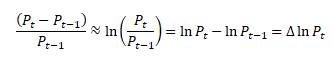
P_t ... cena aktiva v čase t, P_t-1 ... cena aktiva v čase t-1, Δ ... delta ... znak pro absolutní změnu

Dejme tomu, že v posledních dvou obchodních dnech akcie uzavřela na cenách P_t = 10,5 a P_t-1 = 10. Úkolem je odhadnout relativní změnu ceny akcie pomocí přirozeného logaritmu.

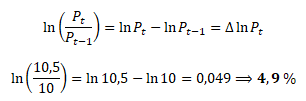
Odhad relativní změny ceny akcie pomocí přirozeného logaritmu je 4,9 %. Výpočet relativní změny klasickým způsobem je 5 %.

Semilogaritmický model

Přirozený logaritmus je často využíván v ekonometrii ke zlinearizování exponenciálních modelů. Dále v semilogaritmických modelech, ve kterých relativní změna závisle proměnné závisí na absolutní změně nezávisle proměnné atd.

Průměrné tempo růstu sledované veličiny se standardně počítá pomocí geometrického průměru. Další možností je odhad tempa růstu pomocí funkce v logaritmicko-lineárním tvaru. Například tempo růstu HDP můžeme odhadnout pomocí modelu

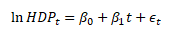
β_j ... parametry funkce, t ... časová proměnná, ε_t ... chyba odhadu

Pomocí metody nejmenších čtverců pak získáme odhad parametrů ekonometrického modelu

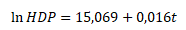
Odhad parametru β₂ říká, že HDP ve sledovaném období rostlo průměrným tempem 1,6 % ročně.