Vlastnosti a předpoklady funkce MNČ

Vlastnostmi odhadové funkce metody nejmenších čtverců (MNČ) jsou nestrannost a vydatnost odhadů. Jsou založené na předpokladech MNČ a charakteristikách vyjadřujících popis náhodných veličin s normálním rozdělením. Jsou-li splněny předpoklady KLRM, jsou splněny i požadované vlastnosti odhadů MNČ. Jinými slovy, můžeme se spolehnout na výsledky odhadnutých modelů a vztáhnout je na celou populaci.

Vlastnosti funkce MNČ se vyjadřují pomocí momentových charakteristik, kterými jsou střední hodnota a kovarianční (rozptylová) matice.

Předpoklady KLRM a náhodná složka

Pro zavedení předpokladů KLRM a odvození momentových charakteristik odhadové funkce MNČ bude vycházet z regresního modelu v maticovém vyjádření

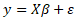
y ... sloupcový vektor n pozorování hodnot závisle proměnné, X ... matice n x (k + 1) pozorování hodnot vysvětlujících proměnných, β ... sloupcový vektor k + 1 neznámých parametrů, ε ... sloupcový vektor n hodnot náhodné složky

Mají-li mít složky odhadu b vektoru neznámých parametrů β optimální vlastnosti, musí být splněny následující předpoklady:

• P₁: E(ε) = 0 - střední hodnota náhodné složky je ve všech pozorováních nulová
• P₂: E(εε^T) = σ²I_n - náhodné složky mají konstantní a konečný rozptyl (= homoskedasticita) a jsou navzájem nekorelované (= sériová nezávislost)
• P₃: E(X^Tε) = 0 - matice hodnot nezávisle proměnných X je nezávislá na náhodné složce, matice X je nestochastická
• P₄: h(X) = k + 1 ≤ n - matice nezávisle proměnných X musí mít plnou hodnost k + 1 - sloupce matice X nejsou lineárně závislé

Z uvedených předpokladů je patrné, že zvláštní pozornost je věnována náhodné složce ε. Náhodná složka hraje důležitou roli v momentových charakteristikách odhadové funkce b a jejím pravděpodobnostním rozdělení. Ke klasickým předpokladům se přidává předpoklad normálního rozdělení náhodné složky s nulovou střední hodnotou a kovarianční maticí

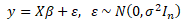
V praxi je kladen velký důraz na sériovou nezávislost a konstantní rozptyl (P₂). Vlastnosti náhodné složky hrají ústřední roli při testování statistických hypotéz (t-test regresních parametrů, F-test regresního modelu), konstrukci intervalů spolehlivosti pro parametry modelu a předpovědo budoucí hodnoty závislé endogenní proměnné y.

Momentové charakteristiky odhadové funkce MNČ

Od normálního rozdělení náhodné složky se odvíjí i rozdělení odhadu b vektoru. Náhodnou veličinu s normálních rozdělením můžeme popsat pomocí vektoru středních hodnot a kovarianční (rozptylové) matice. Na základě výše uvedených předpokladů, můžeme odvodit momentové charakteristiky odhadové funkce

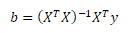
Výchozím krokem k odvození střední hodnoty E(b) a kovarianční matice V(b) je substituce maticového zápisu KLRM do odhadové funkce MNČ

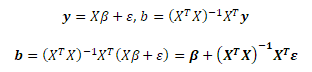
S využitím klasického předpokladu P₁ odvodíme střední hodnotu odhadové funkce MNČ. Vektor β a matice X jsou konstanty, proto i jejich střední hodnoty jsou konstantou.

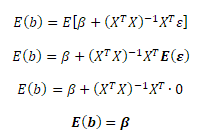
Pomocí předpokladu P₂ odvodíme kovarianční matici odhadové funkce MNČ

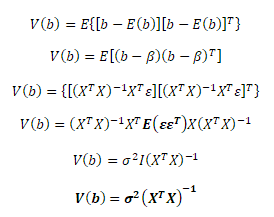
Z kovarianční matice vyplývá, že standardní chyby odhadnutých parametrů jsou dány součinem rozptylu náhodné složky σ² a prvků na diagonále inverzní matice (X^TX)^-1. Toto odvození je velmi důležité pro statistickou verifikaci parametrů.

Odhadová funkce MNČ s normálním rozdělením se zapisuje

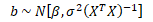
Vlastnosti odhadové funkce MNČ

Jsou-li splněny předpoklady KLRM, mají bodové odhady MNČ požadované vlastnosti, kterými jsou nestrannost odhadů a vydatnost. Uvedené vlastnosti platí pro malé i velké výběry pozorování. V případě nekonečně velkých rozsahů dat (n → ∞) mluvíme o asymptotických nebo limitních vlastnostech (asymptotická nestrannost, asymptotická vydatnost a konzistence).

Odhady b vektoru parametrů β regresního modelu jsou náhodné veličiny. Pro každý výběrový soubor dat nabývají odhady odlišných hodnot. Vztah E(b) = β znamená, že střední hodnota b z různých výběrů dat je rovna β. Odhady MNČ jsou tedy nestranné.

Odhady parametrů MNČ mají nejnižší rozptyl ze všech nestranných odhadových funkcí. Čím větší by byl rozptyl, tím rozptýlenější by byly hodnoty okolo střední hodnoty E(b) = β a tedy vzdálenější od β. Bodové odhady parametrů MNČ mají nízký rozptyl. Proto jsou jejich nestranné odhady také vydatné.

Odhady MNČ jsou konzistentní, pokud vychýlení a rozptyl odhadu s rostoucím rozsahem dat konverguje k nule. Tato vlastnost říká, že s rostoucím rozsahem dat dochází ke zlepšení bodových odhadů MNČ. Obecně platí, že čím větší rozsah dat máme k dispozici, tím kvalitnější je odhad regresního modelu.