Regresní parabola a Cramerovo pravidlo
Publikováno: 17.6.2017

Minimalizační kritérium MNČ, odvození soustavy normálních rovnic pro regresní parabolu, řešení parametrů soustavy pomocí Cramerova pravidla
- regresní parabola
- Sarrusovo pravidlo
- MNČ
V předchozích článcích byly demonstrovány dva způsoby odhadu parametrů výběrové regresní přímky ve tvaru Y = b0 + b1x. Nyní je na programu složitější model výběrové regresní paraboly ve tvaru Y = b0 + b1x + b2x2. Cílem článku je řešení soustavy lineárních rovnic pro regresní parabolu pomocí Cramerova pravidla. Cramerovo pravidlo je metoda, která se používá k řešení soustavy normálních rovnic vytvořené pomocí metody nejmenších čtverců (MNČ).
Soustava rovnic regresní paraboly
Prvním krokem je řešení minimalizačního kritéria MNČ pro již zmíněnou výběrovou regresní parabolu ve tvaru Y = b0 + b1x + b1x2. Kritérium minimalizuje součet čtverců odchylek ∑e2 skutečných hodnot závisle proměnné y od jejich vyrovnaných hodnot Y.
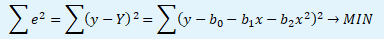
Parciálními derivacemi minimalizačního kritéria podle jednotlivých parametrů a položením rovno nule získáme následující rovnice.
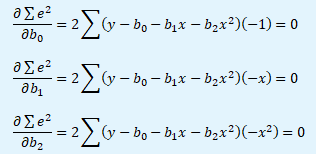
Jednoduchými úpravami je vytvořena soustava rovnic o 3 neznámých regresních parametrech b0, b1 a b2.
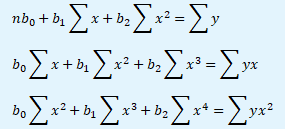
Analogicky lze získat soustavu rovnic pro všechny ostatní regresní funkce.
Cramerovo pravidlo
Cílem článku je odhad parametrů výběrové regresní paraboly pomocí Cramerova pravidla. Konkrétně hledáme řešení řádkového vektoru bT = (b0, b1, b2).
Prvním krokem je sestavení matice soustavy A z prvků normálních rovnic na levé straně n, ∑x, ∑x2, ∑x3 a ∑x4. A vektoru pravých stran s prvky ∑y, ∑yx a ∑x2.
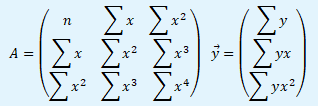
Dalším krokem je vytvoření matic Ai z matice soustavy A záměnou i-tého sloupce s vektorem pravých stran.
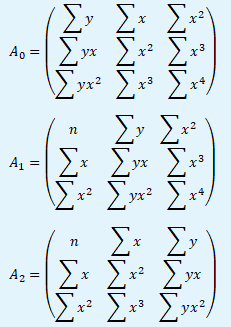
Cramerovo pravidlo je založeno na poměru determinantu odvozené matice Ai a determinantu matice soustavy A. Je-li determinant matice A nenulový (značené detA ≠ 0), pak má soustava jedno řešení, která je dáno následujícím Cramerovým vzorcem.
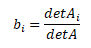
bi ... hledaný i-tý neznámý parametr
detAi ... determinant matice Ai
detA ... determinant matice A
Determinant matice je reálné číslo, které je určitým algoritmem přiřazeno čtvercové matici (n x n). Algoritmus se pro každý řád čtvercové matice liší.
Determinant čtvercové matice řádu n = 3 je řešen pomocí Sarrusova pravidla. Princip Sarrusova pravidla spočívá v opsání prvních dvou řádků matice na pozici čtvrtého a pátého řádku. Poté je pomocí křížového pravidla vypočten determinant matice. Aplikace Sarrusova pravidla je naznačena dále v praktické části článku.
Odhad parametrů regresní paraboly v praxi
Úkolem je odhadnout teoretickou funkci tržeb firmy, která je typická pro nedokonalé konkurenční prostředí. Firma může zvýšit prodej výrobků snížením ceny. Zda však budou celkové tržby růst nebo klesat závisí na cenové elasticitě poptávky pro produkci firmy.
Následující tabulka obsahuje proměnné tržby za prodej vlastních výrobků y a množství prodaných výrobků x. Z těchto proměnných jsou vytvořeny nové proměnné x2, x3, x4, yx a yx2, které potřebujeme pro řešení soustavy normálních rovnic.
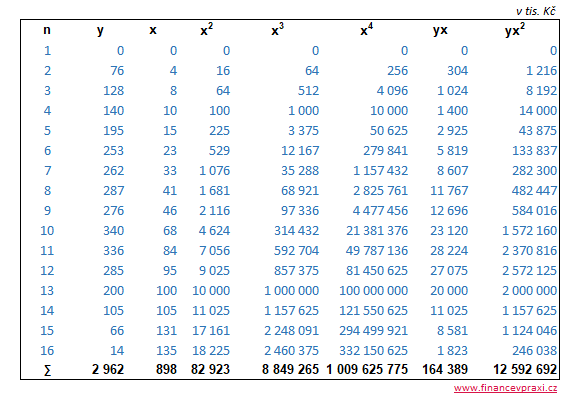
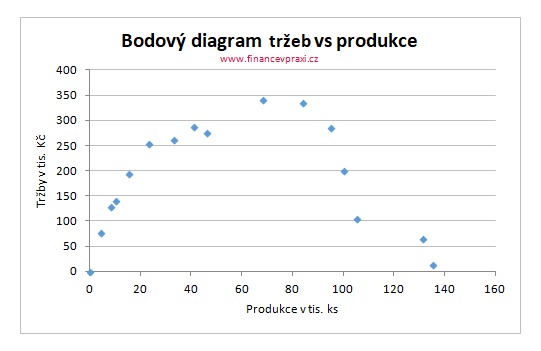
Jelikož regresní parabola popisuje vztah závisle proměnné y a jedné nezávisle proměnné x, můžeme průběh závislosti zobrazit graficky. Z mikroekonomické teorie však již víme, že mezi proměnnými je kvadratický vztah.
Soustava normálních rovnic pro regresní parabolu má následující konkrétní podobu. Hodnoty jsou převzaty ze sumačního řádku tabulky.
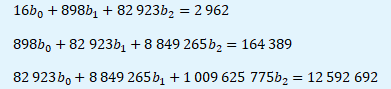
Matici soustavy A vytvoříme z prvků levé strany soustavy rovnic. Determinant matice vypočteme pomocí již zmíněného Sarrusova pravidla, které je naznačeno v boxu níže. Na pozici čtvrtého řádku matice opíšeme první řádek, na pozici pátého řádku opíšeme druhý řádek. Dále se postupuje standardně jako u matice druhé řádu křížovým pravidlem, které je naznačeno barevnými šipkami. Zelené šipky představují součiny s kladným znaménkem, červené šipky součiny se záporným znaménkem.

V dalším kroku vytvoříme z matice soustavy A matici A0 záměnou prvního sloupce s vektorem pravých stran. Determinant matice A0 je vypočten stejným způsobem jako v předchozím kroku.
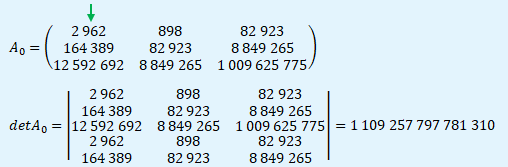
Matice A1 je vytvořena z matice soustavy A záměnou druhého sloupce s vektorem pravých stran a vypočten její determinant.
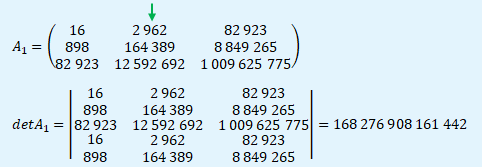
Matice A2 je vytvořena z matice soustavy A záměnou třetího sloupce s vektorem pravých stran a vypočten její determinant.

Posledním krokem je odhad parametrů b0, b1 a b2 regresní paraboly pomocí Cramerových vzorců.

Výběrová regresní parabola má v indexním tvaru následující podobu.

Dosazením hodnot prodaných kusů výrobků za xi do rovnice regresní paraboly získáme vyrovnané hodnoty tržeb firmy. Na základě vyrovnaných hodnot můžeme sestavit graf regresní paraboly.
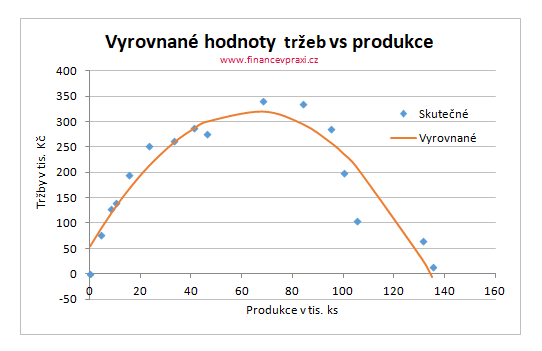
Regresní funkce v MS Excel
- LINREGRESE() - vrátí odhady bj parametrů βj včetně doplňujících testů

