Křivka poptávky a elasticita poptávky

Analýza poptávky je důležitou předehrou před pojednáním o tržní rovnováze. Druhou komponentu trhu tvoří nabídka statků a služeb. V bodě tržní rovnováhy se utváří rovnovážná cena a rovnovážné množství statků a služeb. Jinými slovy, v bodě tržní rovnováhy je množství poptávaných statků a služeb rovno jejich nabídce.

Členění poptávky

Mikroekonomie se zabývá chováním spotřebitelů v rámci maximalizace užitku plynoucí ze spotřeby statků a služeb na jednotlivých trzích (například trh kukuřice, trh automobilů atd.). Z pohledu mikroekonomie se rozlišují individuální a tržní poptávka. Individuální poptávka je poptávkou jednoho spotřebitele na trhu. Zatímco tržní poptávka je dána součtem všech individuálních poptávek na trhu.

Naopak makroekonomie se zabývá agregátní poptávkou. Agregátní poptávka je součtem všech tržních poptávek v ekonomice. Vyjadřuje vztah mezi agregátní cenovou hladinou a agregátním reálných produktem ekonomiky.

Předmětem analýzy poptávky je pouze tzv. efektivní koupěschopná poptávka. Pouze poptávka podložená kupní sílou ekonomických subjektů má vliv na situaci na trhu.

Faktory ovlivňující poptávku

V nejjednodušší podobě je poptávané množství statku X funkcí jeho tržní ceny

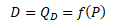
Poptávka je však funkcí i mnoha jiných faktorů. Mezi nejdůležitější faktory patří vlastní cena statku X (P_X), průměrná úroveň důchodu (I), ceny substitutů a komplementů Y (P_Y), počet spotřebitelů na trhu (N), očekávání spotřebitelů (O), preference spotřebitelů a další specifické faktory (ε) nezahrnuté do modelu poptávky.

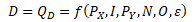
Následující výklad poptávky je zaměřen na vztah poptávaného množství statku Q_D a jeho ceny P. Vztah mezi cenou a poptávaným množstvím je obousměrný. Proto platí, že

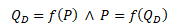
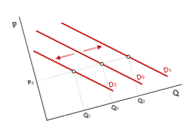
Křivka tržní poptávky

Křivka poptávky vyjadřuje negativní vztah mezi poptávaným množstvím statku Q_D a jeho cenou P. Platí, že s rostoucí cenou klesá poptávané množství a naopak. Křivka poptávky je klesající.

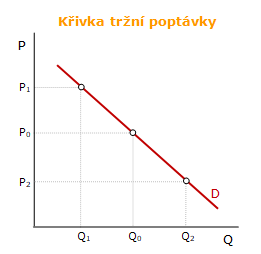
Výchozí situace na poptávkové křivce je poptávané množství Q₀ při ceně P₀. Růst ceny do P₁ snižuje poptávané množství do Q₁. Pokles ceny do P₂ zvyšuje poptávané množství do Q₂. Nižší cena přiláká více kupců a naopak. Tento vztah se označuje jako zákon klesající poptávky. Zákon klesající poptávky si můžeme vysvětlit tím, že růst ceny statku sníží poptávané množství, protože spotřebitelé nahrazují dražší statek levnějším.

Posun poptávkové křivky

Pokud se mění cena statku, dochází pouze k posunu po křivce poptávky. Pokud se však změní jiné faktory dochází k posunu křivky poptávky.

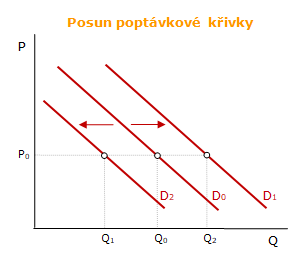
Dojde-li například k růstu reálného důchodu nebo počtu obyvatel, poptávka roste. Graficky to představuje posun poptávkové křivky doprava do D₁. Pokles reálného důchodu nebo pokles počtu obyvatel posunuje křivku poptávky doleva do D₂.

Tvary poptávkové funkce

Pro zachování jednoduchosti výkladu budeme pracovat s lineární funkcí poptávky s negativním sklonem. Lineární poptávku můžeme vyjádřit například jako

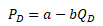
Parametr a vyjadřuje cenu, při které již spotřebitelé nekoupí žádný statek (službu) a opouští daný trh. Parametr b určuje sklon křivky poptávky. Čím větší hodnota parametru, tím strmější je sklon křivky. Podíl parametrů a/b odpovídá maximálnímu množství statku (služby), při kterém jsou uspokojeny potřeby spotřebitelů. Inverzní funkcí k uvedené funkci poptávky je

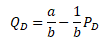
Dalšími elementárními tvary křivky poptávky jsou například kvadratická funkce, hyperbolická funkce a exponenciální funkce.

Odhad reálné poptávky

V reálné ekonomice jsou modely poptávky odhadovány pomocí metody nejmenších čtverců. Na základě funkčních vztahů a počtu vysvětlujících proměnných rozlišujeme lineární (jednofaktorové a vícefaktorové) a nelineární (jednofaktorové a vícefaktorové) modely poptávky. Vícefaktorový model poptávky může mít například následující lineární tvar:

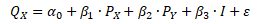
kde α₀ je úrovňová konstanta, β_j jsou koeficienty absolutní pružnosti poptávky, Q_X je poptávka po statku X, P_X je cena statku X (β₁ < 0), P_Y je cena substitutu (β₂ > 0) nebo cena komplementu (β₂ < 0), I je průměrný důchod (β₃ > 0), ε vyjadřuje vliv ostatních faktorů nezahrnutých do modelu

Vztahy v závorkách vyjadřují očekávaná znaménka odhadnutých koeficientů. Koeficient α₀ představuje úroveň poptávky při nulových hodnotách vysvětlujících proměnných P_X, P_Y a I. Koeficienty β_j vyjadřují, o kolik se změní poptávka při jednotkové změně jednotlivých vysvětlujících proměnných. Jednotlivé parametry vysvětlujících proměnných lze vyjádřit pomocí parciálních derivací.

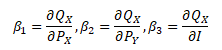
Typickým příklad nelineární funkce poptávky je mocninná Cobb-Douglasova funkce.

Odvození tržní poptávky

Tržní poptávka je dána součtem všech individuálních poptávek spotřebitelů na daném trhu zboží a služeb. V následujícím příkladu je odvozena tržní poptávka na základě 2 individuálních poptávek.

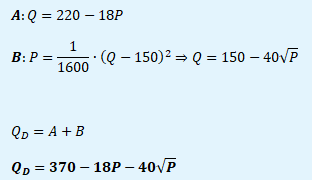
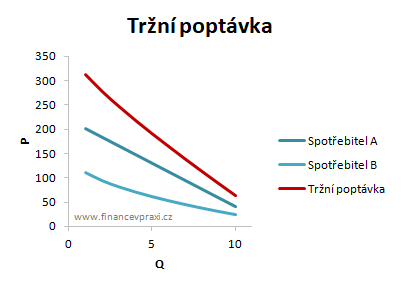
Elasticita poptávky

S analýzou poptávky souvisí pojem elasticita poptávky, která vyjadřuje citlivost reakce spotřebitelů na změny faktorů ovlivňující poptávku. Nejvýznamnější jsou cenová elasticita poptávky, důchodová elasticita poptávky a křížová elasticita poptávky.

Cenová elasticita poptávky

Cenová elasticita poptávky (E_DP) vyjadřuje, o kolik procent se změní poptávané množství statku (Q), pokud se jeho cena (P) změní o jedno procento. Matematicky můžeme cenovou elasticitu zapsat následujícím výrazem

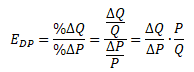
Známe-li %ΔQ a %ΔP, můžeme počítat cenovou elasticitu poptávky uvedeným výrazem. Jinak se výpočet koeficientu elasticity poptávky provádí pomocí obloukové a bodové metody. Stejným způsobem se postupuje i v případě důchodové a křížové elasticity poptávky.

Oblouková metoda počítá elasticitu mezi dvěma body na poptávkové křivce. Používá se pro velké změny Q a P a vyjadřuje průměrnou elasticitu poptávky.

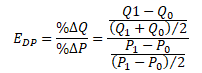
kde %ΔQ a %ΔP vyjadřují průměrné změny, Q₀ je počáteční poptávané množství, Q₁ je poptávané množství po změně ceny, P₀ je počáteční cena, P₁ je cena po změně

Bodová metoda počítá elasticitu v bodě poptávkové křivky. Používá se pro velmi malé změny Q a P a vyjadřuje okamžitou elasticitu poptávky.

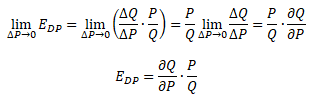
Pokud se ΔP limitně blíží k nule (ΔP → 0) přejde průměrná ΔQ na okamžitou. Jinými slovy, limita výrazu (ΔQ/ΔP) pro ΔP → 0 je derivace funkce Q podle P (∂Q/∂P).

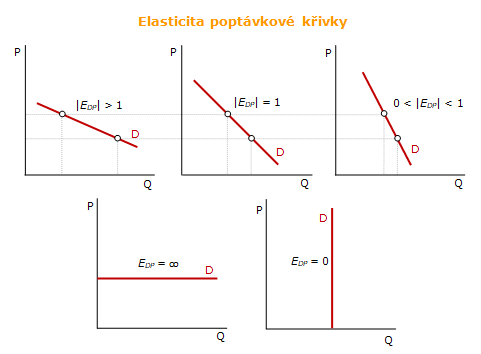
V důsledku inverzního vztahu mezi cenou a poptávaným množství je výsledný koeficient cenové elasticity poptávky záporný. Proto se před vzorec cenové elasticity vkládá záporné znaménko -E_DP nebo se počítá jako absolutní hodnota |E_DP|. Podle výsledné hodnoty koeficientu cenové elasticity poptávky lze rozlišovat poptávku po statku nebo službě následovně:

• elastická poptávka - |E_DP| > 1 - procentní změna ceny vyvolá větší než procentní změnu poptávaného množství
• jednotkově elastická poptávka - |E_DP| = 1 - procentní změna ceny vyvolá procentní změnu poptávaného množství
• neelastická poptávka - 0 < |E_DP| < 1 - procentní změna ceny vyvolá menší než procentní změnu poptávaného množství
• dokonale elastická poptávka - E_DP = ∞ - křivka poptávky je horizontální. Změna poptávaného množství je způsobena jinými faktory než cenou.
• dokonale neelastická poptávka - E_DP = 0 - křivka poptávky je vertikální. Poptávané množství se změnou ceny nemění.

Důchodová elasticita poptávky

Důchodová elasticita poptávky (E_DI) vyjadřuje, o kolik procent se změní poptávané množství (Q) v důsledku procentní změny důchodu (I).

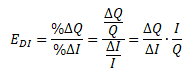
Podle výsledné hodnoty koeficientu důchodové elasticity poptávky rozlišujeme normální a méněcenné statky:

• E_DI > 0 - normální statek
• 0 < E_DI < 1 - nezbytný statek
• E_DI > 1 - luxusní statek
• E_DI < 0 - méněcenný statek

Normální statky jsou statky, jejichž spotřeba s růstem důchodu roste. Méněcenné statky jsou statky, jejichž spotřeba s růstem důchodu klesá.

Křížová elasticita poptávky

Křížová elasticita poptávky (E_DC) vyjadřuje, o kolik procent se změní poptávané množství statku X (Q_X) v důsledku procentní změny ceny statku Y (P_Y).

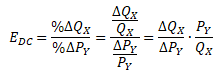
Podle výsledné hodnoty koeficientu křížové elasticity poptávky rozlišujeme substituty a komplementy:

• E_DC > 0 - statky X a Y jsou substituty
• E_DC < 0 - statky X a Y jsou komplementy

Substituty jsou navzájem zaměnitelné statky ve spotřebě (čaj a káva, rohlík a chléb, hovězí a vepřové maso apod.). Komplementy jsou statky, které se ve spotřebě doplňují (těstoviny a parmazán, knihy a papír, auto a benzín apod.).