Model IS-LM: klasický případ
Publikováno: 9.1.2018

Účinnost fiskální a monetární politiky v klasickém případě modelu IS-LM, vertikální křivka LM a multiplikátory hospodářských politik
- klasický případ
- úroková míra
- efekt vytěsnění
Klasický případ v modelu IS-LM představuje pohled neoklasiků a monetaristů na účinnost hospodářské politiky a křivku LM v extrémní situaci, kdy je úroková míra peněžního trhu příliš vysoká a neočekává se další její růst. Při velmi vysoké úrokové míře ekonomické subjekty preferují držbu dluhopisů před penězi. Důvodem je očekávání poklesu úrokové míry a růstu tržních cen dluhopisů, růstu bohatství.
Slovy modelu IS-LM se citlivost spekulační poptávky po reálných peněžních zůstatcích limitně blíží k nule (h → 0). To znamená, že poptávka po penězích nereaguje na změnu úrokové míry. Graficky je křivka LM rovnoběžná s osou y.
Fiskální politika
Fiskální expanze například v podobě růstu vládních výdajů na výstavbu nové dálnice posunuje křivku IS vpravo nahoru do pozice IS1. Posun křivky IS v kombinaci s vertikální křivkou LM způsobil růst úrokové míry z i0 do i1, přičemž reálný produkt a zaměstnanost zůstávají stejné.
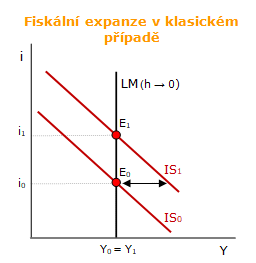
V klasickém pojetí ekonomiky dochází k efektu úplného vytěsnění (oboustranná šipka v grafu) soukromých investic firem a spotřeby domácností. Veřejné výdaje vytěsnily skrze růst úrokové míry soukromé výdaje citlivé na její výši. Fiskální politika je v klasickém případě neúčinná.
Monetární politika
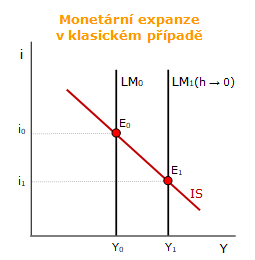
Zvýšení nabídky reálných peněžních zůstatků například operacemi na volném trhu vede k růstu reálného produktu z Y0 do Y1, zaměstnanosti a současně k poklesu úrokové míry z i0 do i1. V tomto případě nedošlo k efektu vytěsnění soukromých výdajů, ale k jejich stimulaci a růstu agregátní poptávky. Monetární expanzivní politika je v klasickém případě maximálně účinná.
Multiplikátory fiskální a monetární politiky
V úvodu kapitoly bylo uvedeno, že koeficient spekulační poptávky po peněžních zůstatcích se v klasickém případě limitně blíží k nule. Proto musíme multiplikátory upravit na podmínky klasického případu pomocí limity funkce.
Následující výraz vyjadřuje multiplikátor fiskální politiky
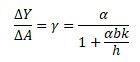
Multiplikátor fiskální politiky je v klasickém případě roven nule. Tím se potvrzuje situace na grafu výše s vertikální křivkou LM, kde veřejné výdaje vytěsnily soukromé autonomní výdaje skrze růst úrokové míry a efekt na reálný produkt byl nulový.
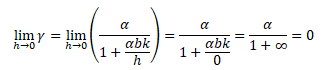
Multiplikátor monetární politiky má následující tvar
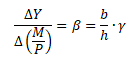
Multiplikátor monetární politiky je v klasickém případě roven výrazu 1/k, který je roven rychlosti obratu peněz z rovnice směny (Y·P = V·M).
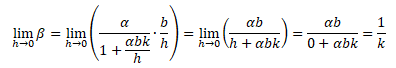
- ČERNÁ, B.: Matematika - lineární algebra. Mendelova zemědělská a lesnická univerzita v Brně 2007, Brno. Páté nezměněné vydání, 130 stran. ISBN 978-80-7375-080-0
- MACH, M.: Markoekonomie II pro magisterské (inženýrské) studium. 1. a 2. část. MELANDRIUM 2001, Slaný. Třetí vydání, 367 stran. ISBN 80-86175-18-9
- PROVAZNÍKOVÁ, R., VOLEJNÍKOVÁ, J.: Makroekonomie - cvičebnice. MELANDRIUM 2003, Slaný. Druhé vydání, 379 stran. ISBN 80-86175-23-5
- REVENDA, Z., MANDEL, M., KODERA, J., MUSÍLEK, P., DVOŘÁK, P., BRADA, J.: Peněžní ekonomie a bankovnictví. Management Press 2004, Praha. Třetí vydání, 634 stran. ISBN 80-7261-031-7
- SAMUELSON, P. A., NORDHAUS, W. D.: Ekonomie. Nakladatelství Svoboda 1995, Praha. Druhé vydání, 1011 stran. ISBN 80-205-0494-X

